Refine search
Actions for selected content:
1 results
LI–YORKE CHAOS ALMOST EVERYWHERE: ON THE PERVASIVENESS OF DISJOINT EXTREMALLY SCRAMBLED SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 03 March 2022, pp. 132-143
- Print publication:
- August 2022
-
- Article
- Export citation
-
We show that there exists a continuous function from the unit Lebesgue interval to itself such that for any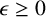
$\epsilon \geq 0$ and any natural number k, any point in its domain has an 
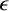$\epsilon $-neighbourhood which, when feasible, contains k mutually disjoint extremally scrambled sets of identical Lebesgue measure, homeomorphic to each other. This result enables a satisfying generalisation of Li–Yorke (topological) chaos and suggests an open (difficult) problem as to whether the result is valid for piecewise linear functions.
