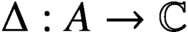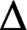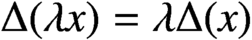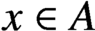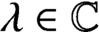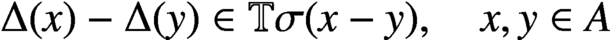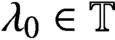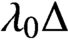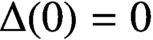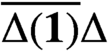Search

Li et al. [‘Weak 2-local isometries on uniform algebras and Lipschitz algebras’, Publ. Mat. 63 (2019), 241–264] generalized the Kowalski–Słodkowski theorem by establishing the following spherical variant: let A be a unital complex Banach algebra and let 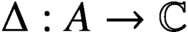$\Delta : A \to \mathbb {C}$ be a mapping satisfying the following properties:

(a) 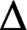$\Delta $ is 1-homogeneous (that is, 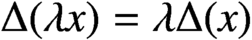$\Delta (\lambda x)=\lambda \Delta (x)$ for all 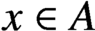$x \in A$, 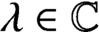$\lambda \in \mathbb C$);
(b) 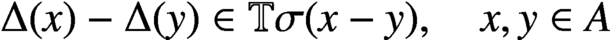$\Delta (x)-\Delta (y) \in \mathbb {T}\sigma (x-y), \quad x,y \in A$.

Then

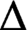$\Delta $ is linear and there exists

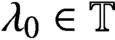$\lambda _{0} \in \mathbb {T}$ such that

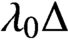$\lambda _{0}\Delta $ is multiplicative. In this note we prove that if (a) is relaxed to

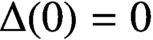$\Delta (0)=0$, then

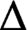$\Delta $ is complex-linear or conjugate-linear and

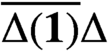$\overline {\Delta (\mathbf {1})}\Delta $ is multiplicative. We extend the Kowalski–Słodkowski theorem as a conclusion. As a corollary, we prove that every 2-local map in the set of all surjective isometries (without assuming linearity) on a certain function space is in fact a surjective isometry. This gives an affirmative answer to a problem on 2-local isometries posed by Molnár [‘On 2-local *-automorphisms and 2-local isometries of B(H)', J. Math. Anal. Appl. 479(1) (2019), 569–580] and also in a private communication between Molnár and O. Hatori, 2018.

Given a separable Banach space E, we construct an extremely non-complex Banach space (i.e. a space satisfying that ‖ Id + T2 ‖ = 1 + ‖ T2 ‖ for every bounded linear operator T on it) whose dual contains E* as an L-summand. We also study surjective isometries on extremely non-complex Banach spaces and construct an example of a real Banach space whose group of surjective isometries reduces to ±Id, but the group of surjective isometries of its dual contains the group of isometries of a separable infinite-dimensional Hilbert space as a subgroup.

Search Results

Refine search

Refine search

Actions for selected content:

2 results

A SPHERICAL VERSION OF THE KOWALSKI–SŁODKOWSKI THEOREM AND ITS APPLICATIONS

Isometries on extremely non-complex Banach spaces

Search Results

Refine search

Refine search

Actions for selected content:

Save Search

2 results

A SPHERICAL VERSION OF THE KOWALSKI–SŁODKOWSKI THEOREM AND ITS APPLICATIONS

Isometries on extremely non-complex Banach spaces