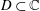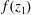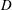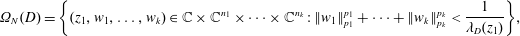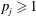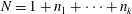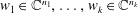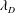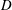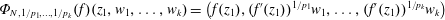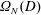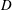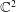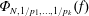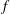Suppose that 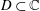 $D\subset \mathbb{C}$ is a simply connected subdomain containing the origin and
$D\subset \mathbb{C}$ is a simply connected subdomain containing the origin and 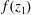 $f(z_{1})$ is a normalized convex (resp., starlike) function on
$f(z_{1})$ is a normalized convex (resp., starlike) function on 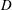 $D$. Let
$D$. Let 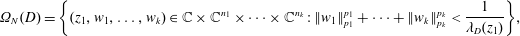 $$\begin{eqnarray}\unicode[STIX]{x1D6FA}_{N}(D)=\bigg\{(z_{1},w_{1},\ldots ,w_{k})\in \mathbb{C}\times \mathbb{C}^{n_{1}}\times \cdots \times \mathbb{C}^{n_{k}}:\Vert w_{1}\Vert _{p_{1}}^{p_{1}}+\cdots +\Vert w_{k}\Vert _{p_{k}}^{p_{k}}<\frac{1}{\unicode[STIX]{x1D706}_{D}(z_{1})}\bigg\},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FA}_{N}(D)=\bigg\{(z_{1},w_{1},\ldots ,w_{k})\in \mathbb{C}\times \mathbb{C}^{n_{1}}\times \cdots \times \mathbb{C}^{n_{k}}:\Vert w_{1}\Vert _{p_{1}}^{p_{1}}+\cdots +\Vert w_{k}\Vert _{p_{k}}^{p_{k}}<\frac{1}{\unicode[STIX]{x1D706}_{D}(z_{1})}\bigg\},\end{eqnarray}$$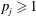 $p_{j}\geqslant 1$,
$p_{j}\geqslant 1$, 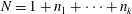 $N=1+n_{1}+\cdots +n_{k}$,
$N=1+n_{1}+\cdots +n_{k}$, 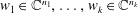 $w_{1}\in \mathbb{C}^{n_{1}},\ldots ,w_{k}\in \mathbb{C}^{n_{k}}$ and
$w_{1}\in \mathbb{C}^{n_{1}},\ldots ,w_{k}\in \mathbb{C}^{n_{k}}$ and 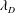 $\unicode[STIX]{x1D706}_{D}$ is the density of the hyperbolic metric on
$\unicode[STIX]{x1D706}_{D}$ is the density of the hyperbolic metric on 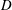 $D$. In this paper, we prove that
$D$. In this paper, we prove that 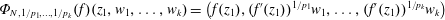 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{N,1/p_{1},\ldots ,1/p_{k}}(f)(z_{1},w_{1},\ldots ,w_{k})=(f(z_{1}),(f^{\prime }(z_{1}))^{1/p_{1}}w_{1},\ldots ,(f^{\prime }(z_{1}))^{1/p_{k}}w_{k})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{N,1/p_{1},\ldots ,1/p_{k}}(f)(z_{1},w_{1},\ldots ,w_{k})=(f(z_{1}),(f^{\prime }(z_{1}))^{1/p_{1}}w_{1},\ldots ,(f^{\prime }(z_{1}))^{1/p_{k}}w_{k})\end{eqnarray}$$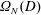 $\unicode[STIX]{x1D6FA}_{N}(D)$. If
$\unicode[STIX]{x1D6FA}_{N}(D)$. If 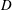 $D$ is the unit disk, then our result reduces to Gong and Liu via a new method. Moreover, we give a new operator for convex mapping construction on an unbounded domain in
$D$ is the unit disk, then our result reduces to Gong and Liu via a new method. Moreover, we give a new operator for convex mapping construction on an unbounded domain in 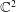 $\mathbb{C}^{2}$. Using a geometric approach, we prove that
$\mathbb{C}^{2}$. Using a geometric approach, we prove that 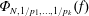 $\unicode[STIX]{x1D6F7}_{N,1/p_{1},\ldots ,1/p_{k}}(f)$ is a spiral-like mapping of type
$\unicode[STIX]{x1D6F7}_{N,1/p_{1},\ldots ,1/p_{k}}(f)$ is a spiral-like mapping of type  $\unicode[STIX]{x1D6FC}$ when
$\unicode[STIX]{x1D6FC}$ when 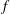 $f$ is a spiral-like function of type
$f$ is a spiral-like function of type  $\unicode[STIX]{x1D6FC}$ on the unit disk.
$\unicode[STIX]{x1D6FC}$ on the unit disk.