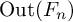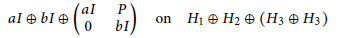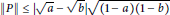Refine search
Actions for selected content:
12 results
11 - Principal Component Analysis and Low-Rank Models
-
- Book:
- Probability and Statistics for Data Science
- Published online:
- 19 June 2025
- Print publication:
- 03 July 2025, pp 433-494
-
- Chapter
- Export citation
3 - Matrix Factorization: Eigendecomposition and SVD
-
- Book:
- Linear Algebra for Data Science, Machine Learning, and Signal Processing
- Published online:
- 01 November 2024
- Print publication:
- 16 May 2024, pp 63-95
-
- Chapter
- Export citation
5 - Spectral Methods
-
- Book:
- Modern Discrete Probability
- Published online:
- 14 December 2023
- Print publication:
- 18 January 2024, pp 256-326
-
- Chapter
- Export citation
LINEAR GROWTH OF TRANSLATION LENGTHS OF RANDOM ISOMETRIES ON GROMOV HYPERBOLIC SPACES AND TEICHMÜLLER SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 1751-1795
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
14 - Normal Matrices and the Spectral Theorem
-
- Book:
- Matrix Mathematics
- Published online:
- 29 September 2023
- Print publication:
- 25 May 2023, pp 277-300
-
- Chapter
- Export citation
1 - Elements of Operator Theory
- from Part One - Background Material
-
- Book:
- Schrödinger Operators: Eigenvalues and Lieb–Thirring Inequalities
- Published online:
- 03 November 2022
- Print publication:
- 17 November 2022, pp 7-65
-
- Chapter
- Export citation
1 - Spectral Representation of Discrete-Time Birth–Death Chains
-
- Book:
- Orthogonal Polynomials in the Spectral Analysis of Markov Processes
- Published online:
- 08 October 2021
- Print publication:
- 21 October 2021, pp 1-56
-
- Chapter
- Export citation
Appendix B - A Type of Compact Symmetric Operator
-
- Book:
- Bounded Gaps Between Primes
- Published online:
- 10 September 2021
- Print publication:
- 25 February 2021, pp 473-479
-
- Chapter
- Export citation
3 - Applications of Spectral Theory to Special Functions
-
-
- Book:
- Lectures on Orthogonal Polynomials and Special Functions
- Published online:
- 07 October 2020
- Print publication:
- 15 October 2020, pp 131-212
-
- Chapter
- Export citation
Factoring a Quadratic Operator as a Product of Two Positive Contractions
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 2 / 01 June 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 354-362
- Print publication:
- 01 June 2016
-
- Article
-
- You have access
- Export citation
Toward a constructive theory of unbounded linear operators
-
- Journal:
- The Journal of Symbolic Logic / Volume 65 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 12 March 2014, pp. 357-370
- Print publication:
- March 2000
-
- Article
- Export citation
Cp-classes of operators in C*-algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 2 / April 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 153-160
- Print publication:
- April 1986
-
- Article
-
- You have access
- Export citation