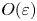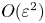Refine search
Actions for selected content:
141 results
A regularized continuum model for travelling waves and dispersive shocks of the granular chain
-
- Journal:
- Journal of Nonlinear Waves / Volume 1 / 2025
- Published online by Cambridge University Press:
- 21 July 2025, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Obliquely interacting solitary waves and wave wakes in free-surface flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 1011 / 25 May 2025
- Published online by Cambridge University Press:
- 14 May 2025, A8
-
- Article
- Export citation
Roughness-induced boundary-layer instability beneath internal solitary waves
-
- Journal:
- Journal of Fluid Mechanics / Volume 1009 / 10 May 2025
- Published online by Cambridge University Press:
- 14 April 2025, A21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transmission and reflection of the dust acoustic wave at an interface in an inhomogeneous dusty plasma
-
- Journal:
- Journal of Plasma Physics / Volume 91 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 31 March 2025, E52
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transition of solitary waves and undular bore from basin to channel with opposing current
- Part of
-
- Journal:
- Journal of Fluid Mechanics / Volume 1006 / 10 March 2025
- Published online by Cambridge University Press:
- 27 February 2025, A1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Damping of solitons by coastal vegetation
-
- Journal:
- Journal of Fluid Mechanics / Volume 1002 / 10 January 2025
- Published online by Cambridge University Press:
- 10 January 2025, A45
-
- Article
- Export citation
Dynamics of solitary waves on a ferrofluid jet: the Hamiltonian framework
-
- Journal:
- Journal of Fluid Mechanics / Volume 1002 / 10 January 2025
- Published online by Cambridge University Press:
- 09 January 2025, A23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Resonant surface waves in an oscillating periodic tank with a submerged hill
-
- Journal:
- Journal of Fluid Mechanics / Volume 999 / 25 November 2024
- Published online by Cambridge University Press:
- 18 November 2024, A69
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Time-periodic generalised solitary waves with a hydraulic fall
-
- Journal:
- Journal of Fluid Mechanics / Volume 998 / 10 November 2024
- Published online by Cambridge University Press:
- 24 October 2024, F1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Graph theoretic methods for assessing the effects of a background shear current on internal solitary waves
-
- Journal:
- Journal of Fluid Mechanics / Volume 997 / 25 October 2024
- Published online by Cambridge University Press:
- 14 October 2024, A37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Self-induced transparency of long water waves over bathymetry: the dispersive shock mechanism
-
- Journal:
- Journal of Fluid Mechanics / Volume 997 / 25 October 2024
- Published online by Cambridge University Press:
- 08 October 2024, A9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
High-level Green–Naghdi model for large-amplitude internal waves in deep water
-
- Journal:
- Journal of Fluid Mechanics / Volume 988 / 10 June 2024
- Published online by Cambridge University Press:
- 03 June 2024, A32
-
- Article
- Export citation
Gas-sheared falling liquid films beyond the absolute instability limit
-
- Journal:
- Journal of Fluid Mechanics / Volume 971 / 25 September 2023
- Published online by Cambridge University Press:
- 25 September 2023, A37
-
- Article
- Export citation
Internal solitary waves generated by a moving bottom disturbance
-
- Journal:
- Journal of Fluid Mechanics / Volume 963 / 25 May 2023
- Published online by Cambridge University Press:
- 22 May 2023, A32
-
- Article
- Export citation
Interaction of mode-one internal solitary waves of opposite polarity in double-pycnocline stratifications
-
- Journal:
- Journal of Fluid Mechanics / Volume 962 / 10 May 2023
- Published online by Cambridge University Press:
- 28 April 2023, A17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cross-shore wind-induced changes to field-scale overturning wave shape
-
- Journal:
- Journal of Fluid Mechanics / Volume 958 / 10 March 2023
- Published online by Cambridge University Press:
- 27 February 2023, A4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonlinear wave attenuation in strongly confined falling liquid films sheared by a laminar counter-current gas flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 954 / 10 January 2023
- Published online by Cambridge University Press:
- 03 January 2023, A19
-
- Article
- Export citation
Large mode-2 internal solitary waves in three-layer flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 953 / 25 December 2022
- Published online by Cambridge University Press:
- 16 December 2022, A42
-
- Article
- Export citation
High-order strongly nonlinear long wave approximation and solitary wave solution. Part 2. Internal waves
-
- Journal:
- Journal of Fluid Mechanics / Volume 952 / 10 December 2022
- Published online by Cambridge University Press:
- 01 December 2022, A41
-
- Article
- Export citation
Modelling falling film flow: an adjustable formulation
-
- Journal:
- Journal of Fluid Mechanics / Volume 952 / 10 December 2022
- Published online by Cambridge University Press:
- 29 November 2022, R3
-
- Article
- Export citation