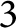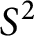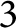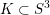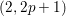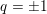Refine search
Actions for selected content:
3 results
A comparison between
 $SL_n$ spider categories
$SL_n$ spider categories
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 07 April 2025, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On framings of links in 3-manifolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 21 September 2020, pp. 752-764
- Print publication:
- December 2021
-
- Article
- Export citation
Double affine Hecke algebras and generalized Jones polynomials
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 7 / July 2016
- Published online by Cambridge University Press:
- 01 April 2016, pp. 1333-1384
- Print publication:
- July 2016
-
- Article
- Export citation