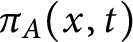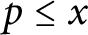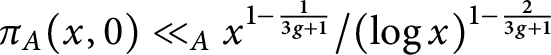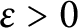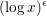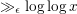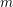Refine search
Actions for selected content:
7 results
IMPROVED UPPER BOUND ON BRUN’S CONSTANT UNDER GRH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 04 July 2025, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POSITIVE DENSITY FOR CONSECUTIVE RUNS OF SUMS OF TWO SQUARES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 21 May 2025, pp. 1995-2046
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Gaussian primes in sparse sets
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 17 June 2025, pp. 181-243
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounds for the distribution of the Frobenius traces associated to products of non-CM elliptic curves
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 07 March 2022, pp. 687-712
- Print publication:
- June 2023
-
- Article
- Export citation
Dense clusters of primes in subsets
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 7 / July 2016
- Published online by Cambridge University Press:
- 01 April 2016, pp. 1517-1554
- Print publication:
- July 2016
-
- Article
-
- You have access
- Export citation
On the Representations of a Number as the Sum of Three Cubes and a Fourth or Fifth Power
-
- Journal:
- Compositio Mathematica / Volume 121 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 04 December 2007, pp. 55-78
- Print publication:
- March 2000
-
- Article
-
- You have access
- Export citation
Differences betweenconsecutive primes
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 76 / Issue 1 / January 1998
- Published online by Cambridge University Press:
- 01 January 1998, pp. 33-69
- Print publication:
- January 1998
-
- Article
- Export citation