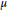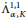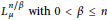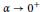The sharpness of various Hardy-type inequalities is well-understood in the reversible Finsler setting; while infinite reversibility implies the failure of these functional inequalities, cf. Kristály et al. [Trans. Am. Math. Soc., 2020]. However, in the remaining case of irreversible manifolds with finite reversibility, there is no evidence on the sharpness of Hardy-type inequalities. In fact, we are not aware of any particular examples where the sharpness persists. In this paper, we present two such examples involving two celebrated inequalities: the classical/weighted Hardy inequality (assuming non-positive flag curvature) and the McKean-type spectral gap estimate (assuming strong negative flag curvature). In both cases, we provide a family of Finsler metric measure manifolds on which these inequalities are sharp. We also establish some sufficient conditions, which guarantee the sharpness of more involved Hardy-type inequalities on these spaces. Our relevant technical tool is a Finslerian extension of the method of Riccati pairs (for proving Hardy inequalities), which also inspires the main ideas of our constructions.

In this paper, we introduce the anisotropic Sobolev capacity with fractional order and develop some basic properties for this new object. Applications to the theory of anisotropic fractional Sobolev spaces are provided. In particular, we give geometric characterizations for a nonnegative Radon measure $\mu $ that naturally induces an embedding of the anisotropic fractional Sobolev class $\dot{\Lambda }_{\alpha ,K}^{1,1}$ into the $\mu $ -based-Lebesgue-space $L_{\mu }^{n/\beta }\,\text{with}\,0<\beta \le n$ . Also, we investigate the anisotropic fractional $\alpha $ -perimeter. Such a geometric quantity can be used to approximate the anisotropic Sobolev capacity with fractional order. Estimation on the constant in the related Minkowski inequality, which is asymptotically optimal as $\alpha \to {{0}^{+}}$ , will be provided.

To realize the automation of biomaterial cutting, the interaction between the blade and biomaterial deserves insight understanding. In this paper, a blade-compression cutting model is developed. The influences from the material properties, deformation, and blade properties on the cutting force are thoroughly explained. An approach to describe the sharpness of a blade is provided and its applicability is experimentally demonstrated. Based on the material property and knife sharpness property, the required force to realize compression cut can be predicted. This provides the reference force trajectory for the automation of biomaterial compression cutting.