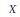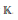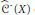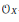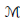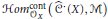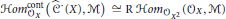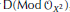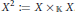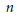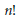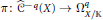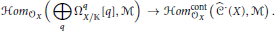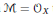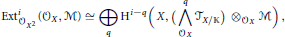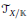Let 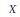 $X$ be a separated finite type scheme over a noetherian base ring
$X$ be a separated finite type scheme over a noetherian base ring 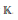 $\mathbb{K}$ . There is a complex
$\mathbb{K}$ . There is a complex 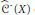 ${{\hat{C}}^{\cdot }}\left( X \right)$ of topological
${{\hat{C}}^{\cdot }}\left( X \right)$ of topological 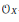 ${{\mathcal{O}}_{X}}$ -modules, called the complete Hochschild chain complex of
${{\mathcal{O}}_{X}}$ -modules, called the complete Hochschild chain complex of 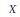 $X$ . To any
$X$ . To any 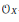 ${{\mathcal{O}}_{X}}$ -module
${{\mathcal{O}}_{X}}$ -module 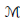 $\mathcal{M}$ —not necessarily quasi-coherent—we assign the complex
$\mathcal{M}$ —not necessarily quasi-coherent—we assign the complex 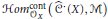 $Hom_{{{\mathcal{O}}_{X}}}^{\text{cont}}\left( {{{\hat{C}}}^{\cdot }}\left( X \right),\,\mathcal{M} \right)$ of continuous Hochschild cochains with values in
$Hom_{{{\mathcal{O}}_{X}}}^{\text{cont}}\left( {{{\hat{C}}}^{\cdot }}\left( X \right),\,\mathcal{M} \right)$ of continuous Hochschild cochains with values in 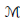 $\mathcal{M}$ . Our first main result is that when
$\mathcal{M}$ . Our first main result is that when 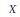 $X$ is smooth over
$X$ is smooth over 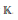 $\mathbb{K}$ there is a functorial isomorphism
$\mathbb{K}$ there is a functorial isomorphism
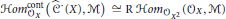 $$Hom_{{{\mathcal{O}}_{X}}}^{\text{cont}}\left( {{C}^{\cdot }}\left( X \right),\,M \right)\,\cong \,\text{R}\,Hom_{{{\mathcal{O}}_{X}}^{2}}^{{}}\,\left( {{\mathcal{O}}_{X}},\,M \right)$$
$$Hom_{{{\mathcal{O}}_{X}}}^{\text{cont}}\left( {{C}^{\cdot }}\left( X \right),\,M \right)\,\cong \,\text{R}\,Hom_{{{\mathcal{O}}_{X}}^{2}}^{{}}\,\left( {{\mathcal{O}}_{X}},\,M \right)$$
in the derived category 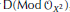 $\text{D}\left( \text{Mod}\,{{\mathcal{O}}_{{{X}^{2}}}} \right)$ , where
$\text{D}\left( \text{Mod}\,{{\mathcal{O}}_{{{X}^{2}}}} \right)$ , where 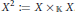 ${{X}^{2}}\,:=\,X\,{{\times }_{\mathbb{K}}}\,X$ .
${{X}^{2}}\,:=\,X\,{{\times }_{\mathbb{K}}}\,X$ .
The second main result is that if 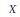 $X$ is smooth of relative dimension
$X$ is smooth of relative dimension 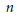 $n$ and
$n$ and 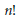 $n!$ is invertible in
$n!$ is invertible in 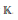 $\mathbb{K}$ , then the standard maps
$\mathbb{K}$ , then the standard maps 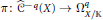 $\text{ }\!\!\pi\!\!\text{ }\,\text{:}\,{{\hat{C}}^{-q}}\left( X \right)\,\to \,\Omega _{X/\mathbb{K}}^{q}$ induce a quasi-isomorphism
$\text{ }\!\!\pi\!\!\text{ }\,\text{:}\,{{\hat{C}}^{-q}}\left( X \right)\,\to \,\Omega _{X/\mathbb{K}}^{q}$ induce a quasi-isomorphism
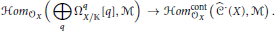 $$Hom_{{{\mathcal{O}}_{X}}}^{{}}\,\left( \underset{q}{\mathop \oplus }\,\,\Omega _{X/\mathbb{K}}^{q}\,\left[ q \right],\,M \right)\,\,\to \,Hom_{{{\mathcal{O}}_{X}}}^{\text{cont}}\left( {{{\hat{C}}}^{\cdot }}\left( X \right),\,M \right).$$
$$Hom_{{{\mathcal{O}}_{X}}}^{{}}\,\left( \underset{q}{\mathop \oplus }\,\,\Omega _{X/\mathbb{K}}^{q}\,\left[ q \right],\,M \right)\,\,\to \,Hom_{{{\mathcal{O}}_{X}}}^{\text{cont}}\left( {{{\hat{C}}}^{\cdot }}\left( X \right),\,M \right).$$
When 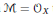 $M\,=\,{{\mathcal{O}}_{X}}$ this is the quasi-isomorphism underlying the Kontsevich Formality Theorem.
$M\,=\,{{\mathcal{O}}_{X}}$ this is the quasi-isomorphism underlying the Kontsevich Formality Theorem.
Combining the two results above we deduce a decomposition of the global Hochschild cohomology
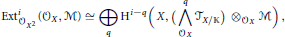 $$\text{Ext}_{{{\mathcal{O}}_{{{X}^{2}}}}}^{i}\,\left( {{\mathcal{O}}_{X}}\,,\,M \right)\,\cong \,\underset{q}{\mathop \oplus }\,\,\,{{\text{H}}^{i-q}}\,\left( X,\,\left( \underset{{{\mathcal{O}}_{X}}}{\overset{q}{\mathop \Lambda }}\,\,{{T}_{X/\mathbb{K}}} \right)\,{{\otimes }_{{{\mathcal{O}}_{X}}}}\,M \right),$$
$$\text{Ext}_{{{\mathcal{O}}_{{{X}^{2}}}}}^{i}\,\left( {{\mathcal{O}}_{X}}\,,\,M \right)\,\cong \,\underset{q}{\mathop \oplus }\,\,\,{{\text{H}}^{i-q}}\,\left( X,\,\left( \underset{{{\mathcal{O}}_{X}}}{\overset{q}{\mathop \Lambda }}\,\,{{T}_{X/\mathbb{K}}} \right)\,{{\otimes }_{{{\mathcal{O}}_{X}}}}\,M \right),$$
where 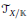 ${{T}_{X/\mathbb{K}}}$ is the relative tangent sheaf.
${{T}_{X/\mathbb{K}}}$ is the relative tangent sheaf.


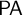


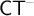

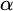
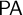
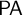
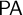
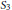

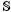 -schemes,
-schemes,