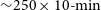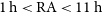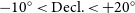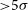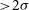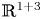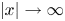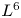Refine search
Actions for selected content:
145 results
Scattering parameters of a wet radome
-
- Journal:
- International Journal of Microwave and Wireless Technologies / Volume 17 / Issue 5 / June 2025
- Published online by Cambridge University Press:
- 27 June 2025, pp. 862-873
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chapter 9 - Ultrasound in Anaesthesia and Intensive Care
- from Section 1 - Nuts and Bolts
-
- Book:
- Robinson and Hall's How to Survive in Anaesthesia
- Published online:
- 09 June 2025
- Print publication:
- 26 June 2025, pp 55-61
-
- Chapter
- Export citation
2 - A Quantum Particle in One Dimension
-
- Book:
- Quantum Mechanics
- Published online:
- 27 June 2025
- Print publication:
- 19 June 2025, pp 26-71
-
- Chapter
- Export citation
5 - The Two-Body Problem
-
- Book:
- Classical Mechanics
- Published online:
- 26 June 2025
- Print publication:
- 19 June 2025, pp 95-135
-
- Chapter
- Export citation

Seismic Wave Propagation Through Random Media
- Monte Carlo Simulation Based on the Radiative Transfer Theory
-
- Published online:
- 31 October 2024
- Print publication:
- 14 November 2024
2 - The Schrödinger Equation
-
- Book:
- A Computational Introduction to Quantum Physics
- Published online:
- 24 April 2024
- Print publication:
- 25 April 2024, pp 16-36
-
- Chapter
- Export citation
Properties of Water in Calcium- and Hexadecyltrimethylammonium-Exchanged Bentonite
-
- Journal:
- Clays and Clay Minerals / Volume 47 / Issue 1 / February 1999
- Published online by Cambridge University Press:
- 28 February 2024, pp. 28-35
-
- Article
- Export citation
Chapter 4 - Mobile Radio Propagation: Large-Scale Path Loss
-
- Book:
- Wireless Communications
- Published online:
- 22 March 2024
- Print publication:
- 08 February 2024, pp 105-176
-
- Chapter
- Export citation
Anomalous Viscosity, Aggregation, and Non-Ergodic Phase of Laponite® RD in a Water–Methanol Binary Solvent
-
- Journal:
- Clays and Clay Minerals / Volume 71 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 01 January 2024, pp. 1-13
-
- Article
- Export citation
3 - The Rivals: Anjha Baras, Adarang and the Scattering of Shahjahanabad
-
- Book:
- Music and Musicians in Late Mughal India
- Published online:
- 09 November 2023
- Print publication:
- 23 November 2023, pp 49-78
-
- Chapter
- Export citation
A census of compact sources at 162 MHz: First data release from the MWA Phase II IPS Survey
-
- Journal:
- Publications of the Astronomical Society of Australia / Volume 39 / 2022
- Published online by Cambridge University Press:
- 23 December 2022, e063
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
8 - The Scattering Transform
-
-
- Book:
- Mathematical Aspects of Deep Learning
- Published online:
- 29 November 2022
- Print publication:
- 22 December 2022, pp 338-399
-
- Chapter
- Export citation
6 - Unbound States
-
- Book:
- Quantum Mechanics
- Published online:
- 11 February 2023
- Print publication:
- 15 September 2022, pp 161-201
-
- Chapter
- Export citation
Collisional rate coefficients for astrophysics
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 18 / Issue S371 / August 2022
- Published online by Cambridge University Press:
- 19 March 2024, pp. 123-132
- Print publication:
- August 2022
-
- Article
-
- You have access
- Export citation
Modeling and electromagnetic analysis of typical environmental clutter based on SMCG
-
- Journal:
- International Journal of Microwave and Wireless Technologies / Volume 15 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 26 April 2022, pp. 322-330
-
- Article
- Export citation
Scattering by PEC half-plane and disk placed on parallel planes
-
- Journal:
- International Journal of Microwave and Wireless Technologies / Volume 15 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 19 April 2022, pp. 311-321
-
- Article
- Export citation
1 - Propagator and Resolvent
-
- Book:
- Advanced Topics in Quantum Mechanics
- Published online:
- 02 December 2021
- Print publication:
- 09 December 2021, pp 1-30
-
- Chapter
- Export citation
11 - Steven Giddings
-
- Book:
- Conversations on Quantum Gravity
- Published online:
- 05 August 2021
- Print publication:
- 26 August 2021, pp 226-239
-
- Chapter
- Export citation
Scattering for critical wave equations with variable coefficients
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 298-316
-
- Article
- Export citation
9 - Modelling the Spectral Energy Distribution of Star-Forming Galaxies with Radiative Transfer Methods
- from Part II - SFR Measurements
-
-
- Book:
- Star-Formation Rates of Galaxies
- Published online:
- 11 May 2021
- Print publication:
- 29 April 2021, pp 204-224
-
- Chapter
- Export citation