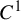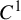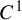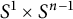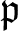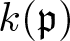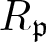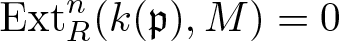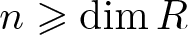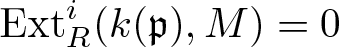Refine search
Actions for selected content:
73 results
5 - School Struggles
- from Part I - Childhood
-
- Book:
- The Artist's Life
- Published online:
- 04 November 2025
- Print publication:
- 20 November 2025, pp 29-34
-
- Chapter
- Export citation
3 - Geometric Rigidity Theory
- from Part I - Maxwell and Structural Mechanics
-
-
- Book:
- The Geometry of Equilibrium
- Published online:
- 03 May 2025
- Print publication:
- 22 May 2025, pp 29-44
-
- Chapter
- Export citation
8 - Rules on Counting, Mechanisms, and States of Self-Stress
- from Part II - Concepts from Maxwell’s Articles on Structural Mechanics
-
-
- Book:
- The Geometry of Equilibrium
- Published online:
- 03 May 2025
- Print publication:
- 22 May 2025, pp 93-106
-
- Chapter
- Export citation
Escitalopram alters tryptophan metabolism, plasma lipopolysaccharide, and the inferred functional potential of the gut microbiome in deer mice showing compulsive-like rigidity
-
- Journal:
- Acta Neuropsychiatrica / Volume 37 / 2025
- Published online by Cambridge University Press:
- 03 April 2025, e60
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On partial rigidity of
 $\mathcal {S}$-adic subshifts
$\mathcal {S}$-adic subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 2724-2764
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chapter 15 - Neuronal Activity in the Basal Ganglia and Thalamus in Patients with Parkinson’s Disease
- from Section 2: - Hypokinetic Movement Disorders
-
-
- Book:
- International Compendium of Movement Disorders
- Published online:
- 07 January 2025
- Print publication:
- 06 February 2025, pp 181-193
-
- Chapter
- Export citation
Rigidity and factivity
-
- Journal:
- Episteme , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
6 - Rigidity and Incomparability
-
- Book:
- The Theory of Countable Borel Equivalence Relations
- Published online:
- 07 November 2024
- Print publication:
- 21 November 2024, pp 51-58
-
- Chapter
- Export citation
Periodic data rigidity of Anosov automorphisms with Jordan blocks
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 19 November 2024, pp. 1129-1160
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rigidity of flat holonomies
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1048-1077
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-rigidity of partially hyperbolic abelian
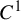 $C^1$-actions on tori
$C^1$-actions on tori
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 09 September 2024, pp. 573-594
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
8 - Faces
-
- Book:
- Polytopes and Graphs
- Published online:
- 14 March 2024
- Print publication:
- 21 March 2024, pp 340-393
-
- Chapter
- Export citation
Sharp gradient estimate, rigidity and almost rigidity of Green functions on non-parabolic RCD(0, N) spaces
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 17 January 2024, pp. 1267-1320
- Print publication:
- August 2025
-
- Article
- Export citation
Chapter 16 - Navigating Meal Planning
- from Part III - Evidence-Informed Considerations for Assessment and Treatment
-
- Book:
- Comorbid Eating Disorders and Obsessive-Compulsive Disorder
- Published online:
- 14 December 2023
- Print publication:
- 21 December 2023, pp 107-115
-
- Chapter
- Export citation
Chapter 17 - Navigating Self-Monitoring
- from Part III - Evidence-Informed Considerations for Assessment and Treatment
-
- Book:
- Comorbid Eating Disorders and Obsessive-Compulsive Disorder
- Published online:
- 14 December 2023
- Print publication:
- 21 December 2023, pp 116-119
-
- Chapter
- Export citation
A rigidity result for the product of spheres
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 13 December 2023, pp. 574-581
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Smooth models for certain fibered partially hyperbolic systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 13 November 2023, pp. 2173-2198
- Print publication:
- August 2024
-
- Article
- Export citation
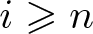
Rigidity of Ext and Tor via flat–cotorsion theory
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 03 November 2023, pp. 1142-1153
-
- Article
- Export citation
Effective rigidity away from the boundary for centrally symmetric billiards
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 28 September 2023, pp. 1741-1756
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HYBRID PARTIAL TYPE THEORY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 29 May 2023, pp. 321-363
- Print publication:
- March 2025
-
- Article
- Export citation