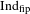Refine search
Actions for selected content:
1 results
Null systems in the non-minimal case
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 17 June 2019, pp. 3420-3437
- Print publication:
- December 2020
-
- Article
- Export citation