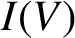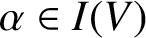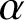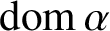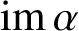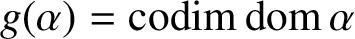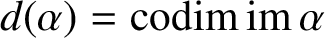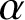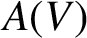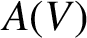Refine search
Actions for selected content:
1 results
INJECTIVE LINEAR TRANSFORMATIONS WITH EQUAL GAP AND DEFECT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 18 May 2021, pp. 106-116
- Print publication:
- February 2022
-
- Article
- Export citation
-
Let V be an infinite-dimensional vector space over a field F and let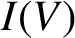
$I(V)$ be the inverse semigroup of all injective partial linear transformations on V. Given 
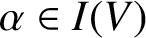$\alpha \in I(V)$, we denote the domain and the range of 
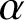$\alpha $ by 
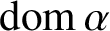${\mathop {\textrm {dom}}}\,\alpha $ and 
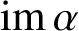${\mathop {\textrm {im}}}\,\alpha $, and we call the cardinals 
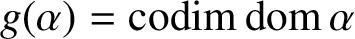$g(\alpha )={\mathop {\textrm {codim}}}\,{\mathop {\textrm {dom}}}\,\alpha $ and 
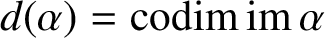$d(\alpha )={\mathop {\textrm {codim}}}\,{\mathop {\textrm {im}}}\,\alpha $ the ‘gap’ and the ‘defect’ of 
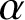$\alpha $. We study the semigroup 
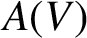$A(V)$ of all injective partial linear transformations with equal gap and defect and characterise Green’s relations and ideals in 
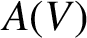$A(V)$. This is analogous to work by Sanwong and Sullivan [‘Injective transformations with equal gap and defect’, Bull. Aust. Math. Soc. 79 (2009), 327–336] on a similarly defined semigroup for the set case, but we show that these semigroups are never isomorphic.
