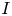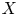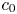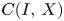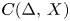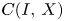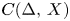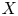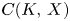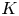Refine search
Actions for selected content:
2 results

Homological Methods in Banach Space Theory
-
- Published online:
- 19 January 2023
- Print publication:
- 26 January 2023
An example regarding Kalton's paper ‘isomorphisms between spaces of vector-valued continuous functions’
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 02 August 2021, pp. 615-619
-
- Article
- Export citation