Refine search
Actions for selected content:
7 results
Totally positive elements with m partitions exist in almost all real quadratic fields
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 21 November 2025, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On
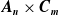 $\boldsymbol{A}_{\boldsymbol{n}} \times \boldsymbol{C}_{\boldsymbol{m}}$-unramified extensions over imaginary quadratic fields
$\boldsymbol{A}_{\boldsymbol{n}} \times \boldsymbol{C}_{\boldsymbol{m}}$-unramified extensions over imaginary quadratic fields
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 29 November 2023, pp. 119-125
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON QUADRATIC FIELDS GENERATED BY POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 29 June 2023, pp. 476-485
- Print publication:
- June 2024
-
- Article
- Export citation
Non-abelian Cohen–Lenstra heuristics over function fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 7 / July 2017
- Published online by Cambridge University Press:
- 12 May 2017, pp. 1372-1390
- Print publication:
- July 2017
-
- Article
- Export citation
On quadratic fields generated by the Shanks sequence
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 3 / October 2009
- Published online by Cambridge University Press:
- 23 September 2009, pp. 719-729
-
- Article
-
- You have access
- Export citation
Corrigendum: on the mean 3-rank of quadratic fields
-
- Journal:
- Compositio Mathematica / Volume 140 / Issue 5 / September 2004
- Published online by Cambridge University Press:
- 04 December 2007, p. 1221
- Print publication:
- September 2004
-
- Article
-
- You have access
- Export citation
A Lower Bound for the Class Number of a Real Quadratic Field of ERD-Type
-
- Journal:
- Canadian Mathematical Bulletin / Volume 37 / Issue 1 / 01 March 1994
- Published online by Cambridge University Press:
- 20 November 2018, pp. 90-96
- Print publication:
- 01 March 1994
-
- Article
-
- You have access
- Export citation











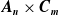

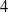

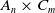
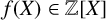
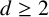
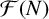
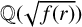
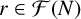
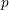
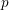
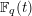
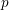
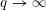
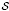 -unit equations as well as bounds for character sums to obtain a lower bound on the number of distinct fields among
-unit equations as well as bounds for character sums to obtain a lower bound on the number of distinct fields among 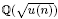 for
for 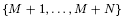 . Fields of this type include the Shanks fields and their generalizations.
. Fields of this type include the Shanks fields and their generalizations.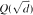 in general, but applied to greatest advantage when
in general, but applied to greatest advantage when 