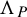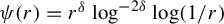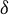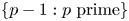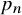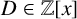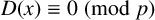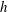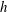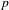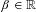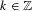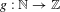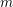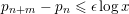Refine search
Actions for selected content:
13 results
1 - Divisibility
-
- Book:
- Essays in Classical Number Theory
- Published online:
- 12 August 2025
- Print publication:
- 28 August 2025, pp 1-115
-
- Chapter
- Export citation
FONCTIONS ADDITIVES EN BASE DE CANTOR LE LONG DES NOMBRES PREMIERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 06 May 2025, pp. 1807-1865
- Print publication:
- September 2025
-
- Article
- Export citation
Exact dimension functions of the prime continued fraction Cantor set
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 14 November 2024, pp. 1757-1776
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unit fractions with shifted prime denominators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 April 2024, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Joint ergodicity of fractional powers of primes
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOLVABILITY OF A SYSTEM OF POLYNOMIAL EQUATIONS MODULO PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 23 March 2022, pp. 404-407
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Irregularities in the Distribution of Prime Numbers in a Beatty Sequence
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 16 December 2019, pp. 738-743
- Print publication:
- December 2020
-
- Article
- Export citation
Zeroes of Polynomials With Prime Inputs and Schmidt’s
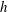 $h$-invariant
$h$-invariant
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 07 February 2019, pp. 805-833
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
PROPRIÉTÉS LOCALES DES CHIFFRES DES NOMBRES PREMIERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 04 April 2017, pp. 189-224
- Print publication:
- January 2019
-
- Article
- Export citation
Dense clusters of primes in subsets
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 7 / July 2016
- Published online by Cambridge University Press:
- 01 April 2016, pp. 1517-1554
- Print publication:
- July 2016
-
- Article
-
- You have access
- Export citation
Radiotherapy scheduling using prime numbers
-
- Journal:
- Journal of Radiotherapy in Practice / Volume 13 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 22 August 2013, pp. 317-321
-
- Article
- Export citation
Factoring and testing primes in small space∗
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 47 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 30 July 2013, pp. 241-259
- Print publication:
- July 2013
-
- Article
- Export citation
ON THE WARING–GOLDBACH PROBLEM FOR FOURTH AND FIFTH POWERS
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 83 / Issue 1 / July 2001
- Published online by Cambridge University Press:
- 20 August 2001, pp. 1-50
- Print publication:
- July 2001
-
- Article
- Export citation