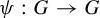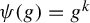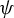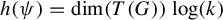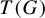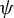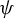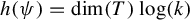Refine search
Actions for selected content:
1 results
The topological entropy of powers on Lie groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 13 December 2022, pp. 3726-3744
- Print publication:
- November 2023
-
- Article
- Export citation
-
In this paper, we address the problem of computing the topological entropy of a map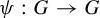
$\psi : G \to G$, where G is a Lie group, given by some power 
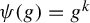$\psi (g) = g^k$, with k a positive integer. When G is abelian, 
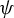$\psi $ is an endomorphism and its topological entropy is given by 
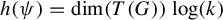$h(\psi ) = \dim (T(G)) \log (k)$, where 
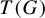$T(G)$ is the maximal torus of G, as shown by Patrão [The topological entropy of endomorphisms of Lie groups. Israel J. Math. 234 (2019), 55–80]. However, when G is not abelian, 
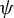$\psi $ is no longer an endomorphism and these previous results cannot be used. Still, 
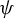$\psi $ has some interesting symmetries, for example, it commutes with the conjugations of G. In this paper, the structure theory of Lie groups is used to show that 
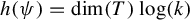$h(\psi ) = \dim (T)\log (k)$, where T is a maximal torus of G, generalizing the formula in the abelian case. In particular, the topological entropy of powers on compact Lie groups with discrete center is always positive, in contrast to what happens to endomorphisms of such groups, which always have null entropy.
