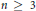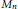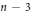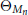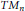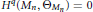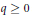Refine search
Actions for selected content:
1 results
On Deformations of the Complex Structure on the Moduli Space of Spatial Polygons
-
- Journal:
- Canadian Mathematical Bulletin / Volume 45 / Issue 3 / 01 September 2002
- Published online by Cambridge University Press:
- 20 November 2018, pp. 417-421
- Print publication:
- 01 September 2002
-
- Article
-
- You have access
- Export citation
-
For an integer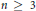
$n\,\ge \,3$ , let 
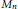${{M}_{n}}$ be the moduli space of spatial polygons with 
$n$ edges. We consider the case of odd $n$ . Then 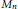${{M}_{n}}$ is a Fano manifold of complex dimension 
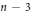$n\,-\,3$ . Let 
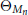${{\Theta }_{{{M}_{n}}}}$ be the sheaf of germs of holomorphic sections of the tangent bundle 
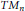$T{{M}_{n}}$ . In this paper, we prove 
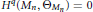${{H}^{q}}\left( {{M}_{n}},\,{{\Theta }_{{{M}_{n}}}} \right)\,=\,0$ for all 
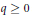$q\,\ge \,0$ and all odd $n$ . In particular, we see that the moduli space of deformations of the complex structure on 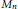${{M}_{n}}$ consists of a point. Thus the complex structure on 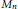${{M}_{n}}$ is locally rigid.
