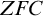Can we quantify over absolutely every set? Absolutists typically affirm, while relativists typically deny, the possibility of unrestricted quantification (in set theory). In the first part of this article, I develop a novel and intermediate philosophical position in the absolutism versus relativism debate in set theory. In a nutshell, the idea is that problematic sentences related to paradoxes cannot be interpreted with unrestricted quantifier domains, while prima facie absolutist sentences (e.g., “no set is contained in the empty set”) are unproblematic in this respect and can be interpreted over a domain containing all sets. In the second part of the paper, I develop a semantic theory that can implement the intermediate position. The resulting framework allows us to distinguish between inherently absolutist and inherently relativist sentences of the language of set theory.

In providing a good foundation for mathematics, set theorists often aim to develop the strongest theories possible and avoid those theories that place undue restrictions on the capacity to possess strength. For example, adding a measurable cardinal to $ZFC$ is thought to give a stronger theory than adding $V=L$ and the latter is thought to be more restrictive than the former. The two main proponents of this style of account are Penelope Maddy and John Steel. In this paper, I’ll offer a third account that is intended to provide a simple analysis of restrictiveness based on the algebraic concept of retraction in the category of theories. I will also deliver some results and arguments that suggest some plausible alternative approaches to analyzing restrictiveness do not live up to their intuitive motivation.

This paper critically examines two arguments against the generic multiverse, both of which are due to W. Hugh Woodin. Versions of the first argument have appeared a number of times in print, while the second argument is relatively novel. We shall investigate these arguments through the lens of two different attitudes one may take toward the methodology and metaphysics of set theory; and we shall observe that the impact of these arguments depends significantly on which of these attitudes is upheld. Our examination of the second argument involves the development of a new (inner) model for Steel’s multiverse theory, which is delivered in the Appendix.