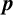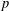Refine search
Actions for selected content:
10 results
RATIONAL REPRESENTATIONS AND RATIONAL GROUP ALGEBRA OF VZ
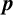 $\boldsymbol {p}$-GROUPS
$\boldsymbol {p}$-GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1-30
- Print publication:
- February 2025
-
- Article
- Export citation
FINITE p-GROUPS AND COCLASS THEORY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 01 December 2020, pp. 164-166
- Print publication:
- August 2021
-
- Article
-
- You have access
- Export citation
Duality between p-groups with three characteristic subgroups and semisimple anti-commutative algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 25 February 2019, pp. 1827-1852
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
COCHAIN SEQUENCES AND THE QUILLEN CATEGORY OF A COCLASS FAMILY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 12 May 2016, pp. 185-204
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
SPECIAL MAXIMAL SUBGROUPS OF
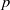 $p$-GROUPS
$p$-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 07 August 2013, pp. 415-419
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Bound for the order for p-elementary subgroups in the plane cremona group over a perfect field
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 19 November 2012, pp. 509-513
-
- Article
-
- You have access
- Export citation
EXISTENCE OF NONINNER AUTOMORPHISMS OF ORDER p IN SOME FINITE p-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 17 September 2012, pp. 272-277
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
2-groups with few conjugacy classes
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 43 / Issue 1 / February 2000
- Published online by Cambridge University Press:
- 20 January 2009, pp. 211-217
-
- Article
-
- You have access
- Export citation
CONJUGACY CLASS SIZES IN FINITE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 251-255
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
Enumerating p-Groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 191-205
- Print publication:
- October 1999
-
- Article
-
- You have access
- Export citation