In this paper, we study ordering properties of vectors of order statistics and sample ranges arising from bivariate Pareto random variables. Assume that $(X_1,X_2)\sim\mathcal{BP}(\alpha,\lambda_1,\lambda_2)$ and $(Y_1,Y_2)\sim\mathcal{BP}(\alpha,\mu_1,\mu_2).$ We then show that $(\lambda_1,\lambda_2)\stackrel{m}{\succ}(\mu_1,\mu_2)$ implies $(X_{1:2},X_{2:2})\ge_{st}(Y_{1:2},Y_{2:2}).$ Under bivariate Pareto distributions, we prove that the reciprocal majorization order between the two vectors of parameters is equivalent to the hazard rate and usual stochastic orders between sample ranges. We also show that the weak majorization order between two vectors of parameters is equivalent to the likelihood ratio and reversed hazard rate orders between sample ranges.

The asymptotic distributions of Brogden's and Lord's modified sample biserial correlation coefficients are derived. The asymptotic variances of these estimators are evaluated for bivariate normal populations and compared to the asymptotic variance of the maximum likelihood estimator.

This paper concerns ordinal responses. An ordered Dirichlet distribution describes prior and posterior beliefs about the cumulative probabilities of response categories. Associating the response categories with intervals of a latent random variable then induces a distribution on the order statistics of that variable. The psychometrician can use the asymptotic theory of order statistics to learn how distributional assumptions about the latent variable effect inference. An example relates the skewness of a latent variable to the proportional odds and proportional hazards models of McCullagh [1980].

In this paper, we use an information theoretic approach called cumulative residual extropy (CRJ) to compare mixed used systems. We establish mixture representations for the CRJ of mixed used systems and then explore the measure and comparison results among these systems. We compare the mixed used systems based on stochastic orders and stochastically ordered conditional coefficients vectors. Additionally, we derive bounds for the CRJ of mixed used systems with independent and identically distributed components. We also propose the Jensen-cumulative residual extropy (JCRJ) divergence to calculate the complexity of systems. To demonstrate the utility of these results, we calculate and compare the CRJ and JCRJ divergence of mixed used systems in the Exponential model. Furthermore, we determine the optimal system configuration based on signature under a criterion function derived from JCRJ in the exponential model.

We establish here an integral inequality for real log-concave functions, which can be viewed as an average monotone likelihood property. This inequality is then applied to examine the monotonicity of failure rates.

In this paper, we introduce a novel way to quantify the remaining inaccuracy of order statistics by utilizing the concept of extropy. We explore various properties and characteristics of this new measure. Additionally, we expand the notion of inaccuracy for ordered random variables to a dynamic version and demonstrate that this dynamic information measure provides a unique determination of the distribution function. Moreover, we investigate specific lifetime distributions by analyzing the residual inaccuracy of the first-order statistics. Nonparametric kernel estimation of the proposed measure is suggested. Simulation results show that the kernel estimator with bandwidth selection using the cross-validation method has the best performance. Finally, an application of the proposed measure on the model selection is provided.

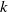More than half a century ago, it was proved that the increasing failure rate (IFR) property is preserved under the formation of k-out-of-n systems (order statistics) when the lifetimes of the components are independent and have a common absolutely continuous distribution function. However, this property has not yet been proved in the discrete case. Here we give a proof based on the log-concavity property of the function $f({{\mathrm{e}}}^x)$. Furthermore, we extend this property to general distribution functions and general coherent systems under some conditions.

The prominence of the Euler allocation rule (EAR) is rooted in the fact that it is the only return on risk-adjusted capital (RORAC) compatible capital allocation rule. When the total regulatory capital is set using the value-at-risk (VaR), the EAR becomes – using a statistical term – the quantile-regression (QR) function. Although the cumulative QR function (i.e., an integral of the QR function) has received considerable attention in the literature, a fully developed statistical inference theory for the QR function itself has been elusive. In the present paper, we develop such a theory based on an empirical QR estimator, for which we establish consistency, asymptotic normality, and standard error estimation. This makes the herein developed results readily applicable in practice, thus facilitating decision making within the RORAC paradigm, conditional mean risk sharing, and current regulatory frameworks.

Almost stochastic dominance has been receiving a great amount of attention in the financial and economic literatures. In this paper, we characterize the properties of almost first-order stochastic dominance (AFSD) via distorted expectations and investigate the conditions under which AFSD is preserved under a distortion transform. The main results are also applied to establish stochastic comparisons of order statistics and receiver operating characteristic curves via AFSD.

In this paper, the multi-state survival signature is first redefined for multi-state coherent or mixed systems with independent and identically distributed (i.i.d.) multi-state components. With the assumption of independence of component lifetimes at different state levels, transformation formulas of multi-state survival signatures of different sizes are established through the use of equivalent systems and a generalized triangle rule for order statistics from several independent and non-identical distributions. The results obtained facilitate stochastic comparisons of multi-state coherent or mixed systems with different numbers of i.i.d. multi-state components. Specific examples are finally presented to illustrate the transformation formulas established here, and also their use in comparing systems of different sizes.

We obtain here sufficient conditions for increasing concave order and location independent more riskier order of lower record values based on stochastic comparisons of minimum order statistics. We further discuss stochastic orderings of lower record spacings. In particular, we show that increasing convex order of adjacent spacings between minimum order statistics is a sufficient condition for increasing convex order of adjacent spacings of their lower records.

The joint signatures of binary-state and multi-state (semi-coherent or mixed) systems with i.i.d. (independent and identically distributed) binary-state components are considered in this work. For the comparison of pairs of binary-state systems of different sizes, transformation formulas of their joint signatures are derived by using the concept of equivalent systems and a generalized triangle rule for order statistics. Similarly, for facilitating the comparison of pairs of multi-state systems of different sizes, transformation formulas of their multi-state joint signatures are also derived. Some examples are finally presented to illustrate and to verify the theoretical results established here.

Providing optimal strategies for maintaining technical systems in good working condition is an important goal in reliability engineering. The main aim of this paper is to propose some optimal maintenance policies for coherent systems based on some partial information about the status of components in the system. For this purpose, in the first part of the paper, we propose two criteria under which we compute the probability of the number of failed components in a coherent system with independent and identically distributed components. The first proposed criterion utilizes partial information about the status of the components with a single inspection of the system, and the second one uses partial information about the status of component failure under double monitoring of the system. In the computation of both criteria, we use the notion of the signature vector associated with the system. Some stochastic comparisons between two coherent systems have been made based on the proposed concepts. Then, by imposing some cost functions, we introduce new approaches to the optimal corrective and preventive maintenance of coherent systems. To illustrate the results, some examples are examined numerically and graphically.

In this paper the behaviour of the failure rate and reversed failure rate of an n-component coherent system is studied, where it is assumed that the lifetimes of the components are independent and have a common cumulative distribution function F. Sufficient conditions are provided under which the system failure rate is increasing and the corresponding reversed failure rate is decreasing. We also study the stochastic and ageing properties of doubly truncated random variables for coherent systems.

We present a method for constructing and interpreting weighted premium principles. The method is based on modifying the underlying risk distribution in such a way that the risk-adjusted expected value (or premium) is greater than the expected value of some conveniently chosen function of claims, which defines the insurer’s perception of the risk. Under some assumptions on the function of claims, the method produces distortion premium principles. We provide several examples under different assumptions on the claim arrival process and different functions of claims, including record claims and kth record claims.

Two definitions of Birnbaum’s importance measure for coherent systems are studied in the case of exchangeable components. Representations of these measures in terms of distribution functions of the ordered component lifetimes are given. As an example, coherent systems with failure-dependent component lifetimes based on the notion of sequential order statistics are considered. Furthermore, it is shown that the two measures are ordered in the case of associated component lifetimes. Finally, the limiting behavior of the measures with respect to time is examined.

In this paper, we consider exponentiated location-scale model and obtain several ordering results between extreme order statistics in various senses. Under majorization type partial order-based conditions, the comparisons are established according to the usual stochastic order, hazard rate order and reversed hazard rate order. Multiple-outlier models are considered. When the number of components are equal, the results are obtained based on the ageing faster order in terms of the hazard rate and likelihood ratio orders. For unequal number of components, we develop comparisons according to the usual stochastic order, hazard rate order, and likelihood ratio order. Numerical examples are considered to illustrate the results.

We obtain the best possible upper bounds for the moments of a single-order statistic from independent, nonnegative random variables, in terms of the population mean. The main result covers the independent identically distributed case. Furthermore, the case of the sample minimum for merely independent (not necessarily identically distributed) random variables is treated in detail.

The signature of a coherent system has been studied extensively in the recent literature. Signatures are particularly useful in the comparison of coherent or mixed systems under a variety of stochastic orderings. Also, certain signature-based closure and preservation theorems have been established. For example, it is now well known that certain stochastic orderings are preserved from signatures to system lifetimes when components have independent and identical distributions. This applies to the likelihood ratio order, the hazard rate order, and the stochastic order. The point of departure of the present paper is the question of whether or not a similar preservation result will hold for the mean residual life order. A counterexample is provided which shows that the answer is negative. Classes of distributions for the component lifetimes for which the latter implication holds are then derived. Connections to the theory of order statistics are also considered.