Refine search
Actions for selected content:
32 results
9 - Delving Deeper: Checking the Underlying Assumptions of the Analysis
-
- Book:
- Multivariable Analysis
- Published online:
- 09 October 2025
- Print publication:
- 23 October 2025, pp 169-186
-
- Chapter
- Export citation
2 - Statistics and Machine Learning for Textual Readability Studies
-
- Book:
- Multilingual Environmental Communications
- Published online:
- 16 May 2025
- Print publication:
- 05 June 2025, pp 23-52
-
- Chapter
- Export citation
10 - Brownian Motion
- from Part II - Pricing by Risk-Neutral Expectation
-
- Book:
- Derivatives Pricing
- Published online:
- 08 July 2025
- Print publication:
- 20 March 2025, pp 243-260
-
- Chapter
- Export citation
Dietary L-arginine for sows minimises the variability of piglets at birth
-
- Journal:
- The Journal of Agricultural Science / Volume 163 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 27 February 2025, pp. 229-237
-
- Article
- Export citation
The Heteroscedastic Graded Response Model with a Skewed Latent Trait: Testing Statistical and Substantive Hypotheses Related to Skewed Item Category Functions
-
- Journal:
- Psychometrika / Volume 77 / Issue 3 / July 2012
- Published online by Cambridge University Press:
- 01 January 2025, pp. 455-478
-
- Article
- Export citation
A Rasch Model for Continuous Ratings
-
- Journal:
- Psychometrika / Volume 52 / Issue 2 / March 1987
- Published online by Cambridge University Press:
- 01 January 2025, pp. 165-181
-
- Article
- Export citation
Estimating the Parameters of the Latent Population Distribution
-
- Journal:
- Psychometrika / Volume 42 / Issue 3 / September 1977
- Published online by Cambridge University Press:
- 01 January 2025, pp. 357-374
-
- Article
- Export citation
2 - Tabular and Graphical Representations
-
- Book:
- Social Behavioral Statistics
- Published online:
- 13 January 2025
- Print publication:
- 28 November 2024, pp 20-39
-
- Chapter
- Export citation
9 - Sampling and Inference
- from Part 2
-
- Book:
- Elementary Statistics for Public Administration
- Published online:
- 01 November 2024
- Print publication:
- 12 September 2024, pp 179-194
-
- Chapter
- Export citation
4 - Descriptive Statistics and the Normal Distribution
-
- Book:
- Applied Regression Models in the Social Sciences
- Published online:
- 17 August 2023
- Print publication:
- 17 August 2023, pp 47-69
-
- Chapter
- Export citation
1 - Basic Concepts in Probability and Statistics
-
- Book:
- Statistical Methods for Climate Scientists
- Published online:
- 03 February 2022
- Print publication:
- 24 February 2022, pp 1-29
-
- Chapter
- Export citation
Number of prime factors with a given multiplicity
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 03 May 2021, pp. 253-269
- Print publication:
- March 2022
-
- Article
- Export citation
2 - Exploratory Spatial Data Analysis Tools and Statistics
-
- Book:
- Spatial Analysis Methods and Practice
- Published online:
- 20 May 2020
- Print publication:
- 11 June 2020, pp 59-146
-
- Chapter
- Export citation
5 - Statistical Approach to Variability in Measurements
-
- Book:
- Experimental Methods for Science and Engineering Students
- Published online:
- 24 August 2019
- Print publication:
- 05 September 2019, pp 85-110
-
- Chapter
- Export citation
PRESERVATION OF LOG-CONCAVITY UNDER CONVOLUTION
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 32 / Issue 4 / October 2018
- Published online by Cambridge University Press:
- 26 September 2017, pp. 567-579
-
- Article
- Export citation
Birth Weight Among Single and Multiple Births on the Åland Islands
-
- Journal:
- Twin Research and Human Genetics / Volume 16 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 18 March 2013, pp. 739-742
-
- Article
-
- You have access
- HTML
- Export citation
The p and the Peas: An Intuitive ModelingApproach to Hypothesis Testing
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 6 / Issue 6 / 2011
- Published online by Cambridge University Press:
- 05 October 2011, pp. 76-95
- Print publication:
- 2011
-
- Article
- Export citation
Gaussian expansions and bounds for the Poisson distribution applied to the Erlang B formula
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 122-143
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Perfectly random sampling of truncated multinormal distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 973-990
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Gaussian polytopes: variances and limit theorems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 297-320
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
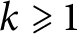
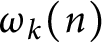
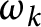
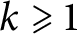
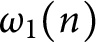
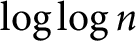
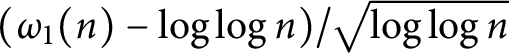
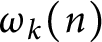
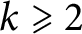
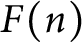
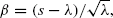 is replaced by Φ(
is replaced by Φ(