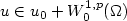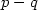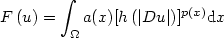Refine search
Actions for selected content:
3 results
Continuity of solutions for the Δϕ-Laplacian operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 11 September 2020, pp. 1355-1382
- Print publication:
- August 2021
-
- Article
- Export citation
Existence and regularity of minimizers of nonconvex integrals with p-q growth
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 13 / Issue 2 / April 2007
- Published online by Cambridge University Press:
- 12 May 2007, pp. 343-358
- Print publication:
- April 2007
-
- Article
- Export citation
Everywhere regularity for vectorial functionals with general growth
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 9 / January 2003
- Published online by Cambridge University Press:
- 15 September 2003, pp. 399-418
- Print publication:
- January 2003
-
- Article
- Export citation