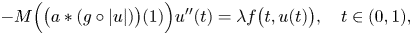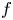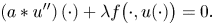Refine search
Actions for selected content:
3 results
A unified topological analysis of variable growth Kirchhoff-type equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
We consider the nonlocal differential equation
\begin{equation*}-A\left(\int_0^1b(1-s)\big(u(s)\big)^{p(s)}\ ds\right)u''(t)=\lambda f\big(t,u(t)\big)\text{, }t\in(0,1),\end{equation*}which is a one-dimensional Kirchhoff-like equation with a nonlocal convolution coefficient. The novelty of our work involves allowing a variable growth term in the nonlocal coefficient. By relating the variable growth problem to a constant growth problem, we are able to deduce the existence of at least one positive solution to the differential equation when equipped with boundary data. Our methodology relies on topological fixed point theory. Because our results treat both the convex and concave regimes, together with both the variable growth and constant growth regimes, our results provide a unified framework for one-dimensional Kirchhoff-type problems.
A unified characterization of convolution coefficients in nonlocal differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-19
-
- Article
- Export citation
-
In loving memory of my beloved miniature dachshund Maddie (16 March 2002 – 16 March 2020). We consider nonlocal differential equations with convolution coefficients of the form
\[{-}M\Big(\big(a*(g\circ |u|)\big)(1)\Big)u''(t)=\lambda f\big(t,u(t)\big),\quad t\in(0,1), \]in the case in which $g$
can satisfy very generalized growth conditions; in addition, $M$
is allowed to be both sign-changing and vanishing. Existence of at least one positive solution to this equation equipped with boundary data is considered. We demonstrate that the nonlocal coefficient $M$
allows the forcing term $f$
to be free of almost all assumptions other than continuity.
Existence and monotonicity of nonlocal boundary value problems: the one-dimensional case
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 23 December 2020, pp. 1-27
- Print publication:
- February 2022
-
- Article
- Export citation
-
We consider nonlocal equations of the general form
By developing a Green's function representation for the solution of the boundary value problem we study existence, uniqueness, and qualitative properties (e.g., positivity or monotonicity) of solutions to these problems. We apply our methods to fractional order differential equations. We also demonstrate an application of our methodology both to convolution equations with nonlocal boundary conditions as well as those with a nonlocal term in the convolution equation itself.
\begin{equation} \left(a*u''\right)(\cdot)+\lambda f\big(\cdot,u(\cdot)\big)=0.\nonumber \end{equation}
