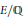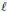Search

For a modular elliptic curve $E/\mathbb{Q}$ , we show a number of links between the primes $\ell $ for which the mod $\ell $ representation of $E/\mathbb{Q}$ has projective dihedral image and congruence primes for the newform associated to $E/\mathbb{Q}$ .

The mod $p$ representation associated to an elliptic curve is called split or non-split dihedral ifits image lies in the normaliser of a split or non-split Cartan subgroup of $\GL_2(\f_p)$, respectively.Let $\xsplit$ and $\xnonsplit$ denote the modular curves which classify elliptic curves with split andnon-split dihedral mod $p$ representation, respectively. We call such curves split and non-split{\it Cartanmodular curves}. The curve $\xsplit$ is isomorphic to the curve $X_0^+(p^2)$. Using the Selberg trace formulafor Hecke operators, we verify that the jacobian of $\xnonsplit$ is isogenous to the new part of the jacobian of$X_0^+(p^2)$.

1991 Mathematics Subject Classification: primary 11G18; secondary 11F72.

Search Results

Refine search

Refine search

Actions for selected content:

2 results

Surjectivity of mod ℓ Representations Attached to Elliptic Curves and Congruence Primes

The Jacobians of non-split Cartan modular curves

Search Results

Refine search

Refine search

Actions for selected content:

Save Search

2 results

Surjectivity of mod ℓ Representations Attached to Elliptic Curves and Congruence Primes

The Jacobians of non-split Cartan modular curves