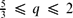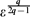Complex materials with internal microstructure such as suspensions and emulsions exhibit time-dependent rheology characterised by viscoelasticity and thixotropy. In many large-scale applications such as turbulent pipe flow, the elastic response occurs on a much shorter time scale than the thixotropy, hence these flows are purely thixotropic. The fundamental dynamics of thixotropic turbulence is poorly understood, particularly the interplay between microstructural state, rheology and turbulence structure. To address this gap, we conduct direct numerical simulations (DNS) of fully developed turbulent pipe flow of a model thixotropic (Moore) fluid as a function of the thixoviscous number $\Lambda$, which characterises the thixotropic kinetic rate relative to turbulence eddy turnover time, ranging from slow ($\Lambda \ll 1$) to fast ($\Lambda \gg 1$) kinetics. Analysis of DNS results in the Lagrangian frame shows that, as expected, in the limits of slow and fast kinetics, these time-dependent flows behave as time-independent purely viscous (generalised Newtonian) analogues. For intermediate kinetics ($\Lambda \sim 1$), the rheology is governed by a path integral of the thixotropic fading memory kernel over the distribution of Lagrangian shear history, the latter of which is modelled via a simple stochastic model for the radially non-stationary pipe flow. The DNS computations based on this effective viscosity closure exhibit excellent agreement with the fully thixotropic model for $\Lambda =1$, indicating that the purely viscous (generalised Newtonian) analogue persists for arbitrary values of $\Lambda \in (0,\infty ^+)$ and across nonlinear rheology models. These results significantly simplify our understanding of turbulent thixotropic flow, and provide insights into the structure of these complex time-dependent flows.

We consider a non-stationary incompressible non-Newtonian Stokes system in a porous medium with characteristic size of the pores ϵ and containing a thin fissure of width ηϵ. The viscosity is supposed to obey the power law with flow index $\frac{5}{3}\leq q\leq 2$. The limit when size of the pores tends to zero gives the homogenized behaviour of the flow. We obtain three different models depending on the magnitude ηϵ with respect to ϵ: if ηϵ ≪ $\varepsilon^{q\over 2q-1}$ the homogenized fluid flow is governed by a time-dependent non-linear Darcy law, while if ηϵ ≫ $\varepsilon^{q\over 2q-1}$ is governed by a time-dependent non-linear Reynolds problem. In the critical case, ηϵ ≈ $\varepsilon^{q\over 2q-1}$, the flow is described by a time-dependent non-linear Darcy law coupled with a time-dependent non-linear Reynolds problem.

This is the second part of the paper for a Non-Newtonian flow. Dual combined Finite Element Methods are used to investigate the littleparameter-dependent problem arising in a nonliner three field version of the Stokes system for incompressible fluids, where the viscosity obeys a general law including the Carreau's law and the Power law. Certain parameter-independent error bounds are obtained which solved the problem proposed by Baranger in [4] in a unifying way. We also give somestable finite element spaces by exemplifying the abstract B-B inequality. The continuous approximation for the extra stress is achieved as a by-product of the new method.