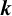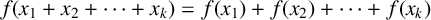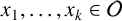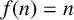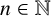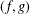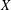Refine search
Actions for selected content:
6 results
Mean values of multiplicative functions and applications to residue-class distribution
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 712-730
-
- Article
- Export citation
ON A
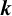 $\boldsymbol {k}$-ADDITIVE UNIQUENESS SET FOR MULTIPLICATIVE FUNCTIONS
$\boldsymbol {k}$-ADDITIVE UNIQUENESS SET FOR MULTIPLICATIVE FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 209-214
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Appendix D - A Brun–Titchmarsh Inequality
-
- Book:
- Bounded Gaps Between Primes
- Published online:
- 10 September 2021
- Print publication:
- 25 February 2021, pp 492-501
-
- Chapter
- Export citation
A note on multiplicative functions on progressions to large moduli
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 December 2017, pp. 63-77
- Print publication:
- February 2018
-
- Article
- Export citation
CONTINUOUS ON RAYS SOLUTIONS OF A GOŁA̧B–SCHINZEL TYPE EQUATION
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 15 December 2014, pp. 273-277
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
COUNTING SYMMETRIC COLOURINGS OF THE VERTICES OF A REGULAR POLYGON
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 10 January 2014, pp. 1-8
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation