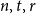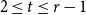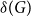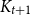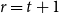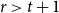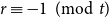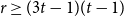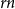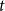Refine search
Actions for selected content:
1 results
Complete subgraphs in a multipartite graph
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 13 June 2022, pp. 1092-1101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
In 1975 Bollobás, Erdős, and Szemerédi asked the following question: given positive integers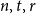
$n, t, r$ with 
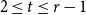$2\le t\le r-1$, what is the largest minimum degree 
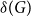$\delta (G)$ among all 
$r$-partite graphs 
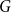$G$ with parts of size 
$n$ and which do not contain a copy of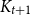 
$K_{t+1}$? The 
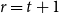$r=t+1$ case has attracted a lot of attention and was fully resolved by Haxell and Szabó, and Szabó and Tardos in 2006. In this article, we investigate the 
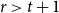$r\gt t+1$ case of the problem, which has remained dormant for over 40 years. We resolve the problem exactly in the case when 
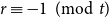$r \equiv -1 \pmod{t}$, and up to an additive constant for many other cases, including when 
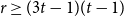$r \geq (3t-1)(t-1)$. Our approach utilizes a connection to the related problem of determining the maximum of the minimum degrees among the family of balanced 
$r$-partite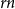 
$rn$-vertex graphs of chromatic number at mos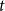t 
$t$.
