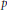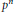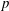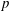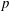Refine search
Actions for selected content:
9 results
Motivic Vitushkin invariants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 20 August 2025, pp. 959-992
- Print publication:
- May 2025
-
- Article
- Export citation
ON THE COMMUTATIVITY OF PULL-BACK AND PUSH-FORWARD FUNCTORS ON MOTIVIC CONSTRUCTIBLE FUNCTIONS
-
- Journal:
- The Journal of Symbolic Logic / Volume 84 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 14 May 2019, pp. 1252-1278
- Print publication:
- September 2019
-
- Article
- Export citation
Generalized Euler characteristic in power-bounded T-convex valued fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 12 / December 2017
- Published online by Cambridge University Press:
- 14 September 2017, pp. 2591-2642
- Print publication:
- December 2017
-
- Article
- Export citation
p-adic and Motivic Measure on Artin n-stacks
-
- Journal:
- Canadian Journal of Mathematics / Volume 67 / Issue 6 / 01 December 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1219-1246
- Print publication:
- 01 December 2015
-
- Article
-
- You have access
- Export citation
The
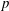 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-cyclic McKay correspondence via motivic integration
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-cyclic McKay correspondence via motivic integration
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 7 / July 2014
- Published online by Cambridge University Press:
- 10 June 2014, pp. 1125-1168
- Print publication:
- July 2014
-
- Article
- Export citation
The arc space of horospherical varieties and motivic integration
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 8 / August 2013
- Published online by Cambridge University Press:
- 19 June 2013, pp. 1327-1352
- Print publication:
- August 2013
-
- Article
- Export citation
Motivic Haar Measure on Reductive Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 58 / Issue 1 / 01 February 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 93-114
- Print publication:
- 01 February 2006
-
- Article
-
- You have access
- Export citation
Motivic invariants of arc-symmetric sets and blow-Nash equivalence
-
- Journal:
- Compositio Mathematica / Volume 141 / Issue 3 / May 2005
- Published online by Cambridge University Press:
- 21 April 2005, pp. 655-688
- Print publication:
- May 2005
-
- Article
-
- You have access
- Export citation
Motivic Integration, Quotient Singularities and the McKay Correspondence
-
- Journal:
- Compositio Mathematica / Volume 131 / Issue 3 / May 2002
- Published online by Cambridge University Press:
- 04 December 2007, pp. 267-290
- Print publication:
- May 2002
-
- Article
-
- You have access
- Export citation