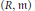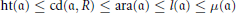Refine search
Actions for selected content:
3 results
On Polynomial Maximum Entropy Method for Classical Moment Problem
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 21 December 2015, pp. 117-127
- Print publication:
- February 2016
-
- Article
- Export citation
On Set Theoretically and Cohomologically Complete Intersection Ideals
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 3 / 01 September 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 477-484
- Print publication:
- 01 September 2014
-
- Article
-
- You have access
- Export citation
Value distribution of certain monomials of algebroid functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 3 / June 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 398-404
- Print publication:
- June 1997
-
- Article
-
- You have access
- Export citation