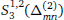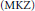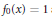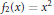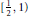Refine search
Actions for selected content:
5 results
Modulus of continuity of invariant densities and entropies for piecewise expanding maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 07 April 2025, pp. 2976-2991
- Print publication:
- October 2025
-
- Article
- Export citation
10 - Minimax Polynomial Approximation
- from Part II - Constructive Approximation Theory
-
- Book:
- Classical Numerical Analysis
- Published online:
- 29 September 2022
- Print publication:
- 20 October 2022, pp 266-299
-
- Chapter
- Export citation
Mappings of Lp-integrable distortion: regularity of the inverse
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 16 May 2016, pp. 647-663
- Print publication:
- June 2016
-
- Article
- Export citation
On the Approximation of the Derivatives of Spline Quasi-Interpolation in Cubic Spline Space
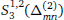
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 7 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 28 May 2015, pp. 1-22
- Print publication:
- February 2014
-
- Article
- Export citation
MKZ Type Operators Providing a Better Estimation on [1/2, 1)
-
- Journal:
- Canadian Mathematical Bulletin / Volume 50 / Issue 3 / 01 September 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 434-439
- Print publication:
- 01 September 2007
-
- Article
-
- You have access
- Export citation
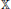 be an open set in ℝ
be an open set in ℝ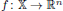 is a Sobolev homeomorphism. We study the regularity of
is a Sobolev homeomorphism. We study the regularity of