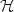Refine search
Actions for selected content:
4 results
Minimizing movements for forced anisotropic mean curvature flow of partitions with mobilities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 17 August 2020, pp. 1135-1170
- Print publication:
- August 2021
-
- Article
-
- You have access
- Open access
- Export citation
Minimizing movements for oscillating energies: the critical regime
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 719-737
- Print publication:
- June 2019
-
- Article
- Export citation
Minimizing movements for dislocation dynamics with a mean curvature term
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 15 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 23 January 2009, pp. 214-244
- Print publication:
- January 2009
-
- Article
- Export citation
Gradient flows of non convex functionals in Hilbert spaces and applications
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 12 / Issue 3 / July 2006
- Published online by Cambridge University Press:
- 20 June 2006, pp. 564-614
- Print publication:
- July 2006
-
- Article
- Export citation