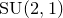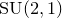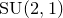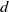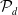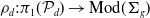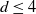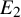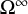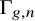Refine search
Actions for selected content:
24 results
A MATROID PROPERTY OF FILLING CURVES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 21 July 2025, pp. 1-5
-
- Article
- Export citation
Random walks and contracting elements I: deviation inequality and limit laws
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 17 September 2025, pp. 1512-1575
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics on the
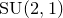 $\mathrm {SU}(2,1)$-character variety of the one-holed torus
$\mathrm {SU}(2,1)$-character variety of the one-holed torus
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rigidity of mapping class groups MOD powers of twists
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 07 April 2025, pp. 1-71
-
- Article
- Export citation
A note on separability in outer automorphism groups
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 04 February 2025, pp. 705-711
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the monodromy group of the family of smooth quintic plane curves
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 28 November 2024, pp. 163-184
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Volume and Euler classes in bounded cohomology of transformation groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 02 October 2024, pp. 34-49
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FINITENESS OF CANONICAL QUOTIENTS OF DEHN QUANDLES OF SURFACES
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 11 March 2024, pp. 317-334
- Print publication:
- June 2025
-
- Article
- Export citation
THE CERESA CLASS: TROPICAL, TOPOLOGICAL AND ALGEBRAIC
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 21 December 2023, pp. 2175-2215
- Print publication:
- September 2024
-
- Article
- Export citation
Parametrised moduli spaces of surfaces as infinite loop spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Right-angled Artin groups as normal subgroups of mapping class groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 27 July 2021, pp. 1807-1852
- Print publication:
- August 2021
-
- Article
- Export citation
ALGEBRAIC ISOMONODROMIC DEFORMATIONS AND THE MAPPING CLASS GROUP
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 18 November 2019, pp. 1497-1545
- Print publication:
- September 2021
-
- Article
- Export citation
10 - Uniform quasiconvexity of the disc graphs in the curve graphs
- from Part Three - Research Articles
-
- Book:
- Beyond Hyperbolicity
- Published online:
- 22 June 2019
- Print publication:
- 11 July 2019, pp 223-231
-
- Chapter
- Export citation
4 - A survey on Morse boundaries and stability
- from Part Two - Expository Articles
-
- Book:
- Beyond Hyperbolicity
- Published online:
- 22 June 2019
- Print publication:
- 11 July 2019, pp 83-116
-
- Chapter
- Export citation
2 - Semihyperbolicity
- from Part One - LECTURES
-
- Book:
- Beyond Hyperbolicity
- Published online:
- 22 June 2019
- Print publication:
- 11 July 2019, pp 25-64
-
- Chapter
- Export citation
1 - Notes on coarse median spaces
- from Part One - LECTURES
-
- Book:
- Beyond Hyperbolicity
- Published online:
- 22 June 2019
- Print publication:
- 11 July 2019, pp 3-24
-
- Chapter
-
- You have access
- Export citation
5 - What is a hierarchically hyperbolic space?
- from Part Two - Expository Articles
-
- Book:
- Beyond Hyperbolicity
- Published online:
- 22 June 2019
- Print publication:
- 11 July 2019, pp 117-148
-
- Chapter
- Export citation
Surface groups, infinite generating sets, and stable commutator length
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 23 April 2019, pp. 2379-2386
- Print publication:
- October 2020
-
- Article
- Export citation
Diffeomorphism groups of tame Cantor sets and Thompson-like groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 5 / May 2018
- Published online by Cambridge University Press:
- 03 April 2018, pp. 1066-1110
- Print publication:
- May 2018
-
- Article
- Export citation
IMAGES OF QUANTUM REPRESENTATIONS OF MAPPING CLASS GROUPS AND DUPONT–GUICHARDET–WIGNER QUASI-HOMOMORPHISMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 27 January 2016, pp. 277-304
- Print publication:
- April 2018
-
- Article
- Export citation