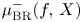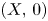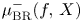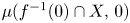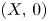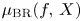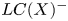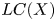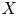Refine search
Actions for selected content:
1 results
The relative Bruce–Roberts number of a function on a hypersurface
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 19 August 2021, pp. 662-674
-
- Article
- Export citation
-
We consider the relative Bruce–Roberts number $\mu _{\textrm {BR}}^{-}(f,\,X)$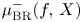
of a function on an isolated hypersurface singularity $(X,\,0)$
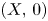. We show that $\mu _{\textrm {BR}}^{-}(f,\,X)$
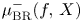is equal to the sum of the Milnor number of the fibre $\mu (f^{-1}(0)\cap X,\,0)$
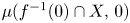plus the difference $\mu (X,\,0)-\tau (X,\,0)$
between the Milnor and the Tjurina numbers of $(X,\,0)$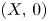
. As an application, we show that the usual Bruce–Roberts number $\mu _{\textrm {BR}}(f,\,X)$
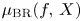is equal to $\mu (f)+\mu _{\textrm {BR}}^{-}(f,\,X)$
. We also deduce that the relative logarithmic characteristic variety $LC(X)^{-}$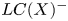
, obtained from the logarithmic characteristic variety $LC(X)$
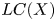by eliminating the component corresponding to the complement of $X$
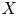in the ambient space, is Cohen–Macaulay.
