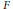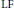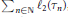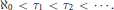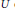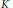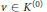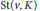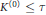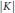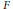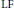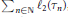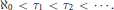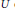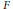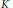Let $F$ be a non-separable $\text{LF}$ -space homeomorphic to the direct sum ${{\sum }_{n\in \text{N}}}\,{{\ell }_{2}}\left( {{\tau }_{n}} \right)$ , where ${{\aleph }_{0}}<{{\tau }_{1}}<{{\tau }_{2}}<\cdot \cdot \cdot $ . It is proved that every open subset $U$ of $F$ is homeomorphic to the product $\left| K \right|\,\times \,F$ for some locally finite-dimensional simplicial complex $K$ such that every vertex 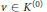$v\,\in \,{{K}^{\left( 0 \right)}}$ has the star 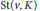$\text{St}\left( v,\,K \right)$ with card $\text{St}{{\left( v,K \right)}^{\left( 0 \right)}}<\tau =\sup {{\tau }_{n}}$ (and card 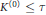${{K}^{\left( 0 \right)}}\le \tau $ ), and, conversely, if 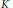$K$ is such a simplicial complex, then the product $\left| K \right|\,\times \,F$ can be embedded in 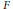$F$ as an open set, where 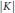$\left| K \right|$ is the polyhedron of 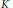$K$ with the metric topology.

The central area of investigation is in the isolation of conditions on mappings which leave invariant the classes of locally finite-dimensional metric spaces and strongly countable-dimensional metric spaces. Examples of such properties are open and closed with discrete point-inverses, open and finite-to-one, or open, closed, and countable-to-one.