We investigate the primitive recursive content of linear orders. We prove that the punctual degrees of rigid linear orders, the order of the integers $\mathbb {Z}$, and the order of the rationals $\mathbb {Q}$ embed the diamond (preserving supremum and infimum). In the cases of rigid orders and the order $\mathbb {Z}$, we further extend the result to embed the atomless Boolean algebra; we leave the case of $\mathbb {Q}$ as an open problem. We also show that our results for the rigid orders, in fact, work for orders having a computable infinite invariant rigid sub-order.

We show that all large enough positive integral surgeries on algebraic knots bound a 4-manifold with a negative definite plumbing tree, which we describe explicitly. Then we apply the lattice embedding obstruction coming from Donaldson’s Theorem to classify the ones of the form $S^3_n(T(p_1,k_1p_1+1; p_2, k_2p_2\pm 1))$ that also bound rational homology 4-balls.

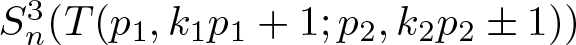
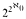We investigate the structure of the Medvedev lattice as a partial order. We prove that every interval in the lattice is either finite, in which case it is isomorphic to a finite Boolean algebra, or contains an antichain of size . the size of the lattice itself. We also prove that it is consistent with ZFC that the lattice has chains of size . and in fact that these big chains occur in every infinite interval. We also study embeddings of lattices and algebras. We show that large Boolean algebras can be embedded into the Medvedev lattice as upper semilattices, but that a Boolean algebra can be embedded as a lattice only if it is countable. Finally we discuss which of these results hold for the closely related Muchnik lattice.