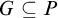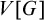Refine search
Actions for selected content:
4 results
THE ORDERING PRINCIPLE AND DEPENDENT CHOICE
- Part of
-
- Journal:
- Bulletin of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON EASTON SUPPORT ITERATION OF PRIKRY-TYPE FORCING NOTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 25 October 2023, pp. 968-1013
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON RESTRICTIONS OF ULTRAFILTERS FROM GENERIC EXTENSIONS TO GROUND MODELS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 25 March 2022, pp. 169-190
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Iterations for Diagonally Dominant Matrices
-
- Journal:
- Canadian Mathematical Bulletin / Volume 19 / Issue 3 / 01 September 1976
- Published online by Cambridge University Press:
- 20 November 2018, pp. 375-377
- Print publication:
- 01 September 1976
-
- Article
-
- You have access
- Export citation