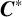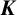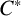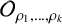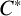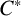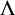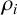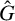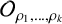We introduce certain 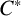 $C^*$-algebras and k-graphs associated to k finite-dimensional unitary representations
$C^*$-algebras and k-graphs associated to k finite-dimensional unitary representations  $\rho _1,\ldots ,\rho _k$ of a compact group G. We define a higher rank Doplicher-Roberts algebra
$\rho _1,\ldots ,\rho _k$ of a compact group G. We define a higher rank Doplicher-Roberts algebra 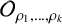 $\mathcal {O}_{\rho _1,\ldots ,\rho _k}$, constructed from intertwiners of tensor powers of these representations. Under certain conditions, we show that this
$\mathcal {O}_{\rho _1,\ldots ,\rho _k}$, constructed from intertwiners of tensor powers of these representations. Under certain conditions, we show that this 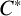 $C^*$-algebra is isomorphic to a corner in the
$C^*$-algebra is isomorphic to a corner in the 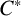 $C^*$-algebra of a row-finite rank k graph
$C^*$-algebra of a row-finite rank k graph 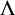 $\Lambda $ with no sources. For G finite and
$\Lambda $ with no sources. For G finite and 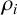 $\rho _i$ faithful of dimension at least two, this graph is irreducible, it has vertices
$\rho _i$ faithful of dimension at least two, this graph is irreducible, it has vertices 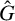 $\hat {G}$ and the edges are determined by k commuting matrices obtained from the character table of the group. We illustrate this with some examples when
$\hat {G}$ and the edges are determined by k commuting matrices obtained from the character table of the group. We illustrate this with some examples when 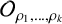 $\mathcal {O}_{\rho _1,\ldots ,\rho _k}$ is simple and purely infinite, and with some K-theory computations.
$\mathcal {O}_{\rho _1,\ldots ,\rho _k}$ is simple and purely infinite, and with some K-theory computations.
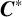 $\boldsymbol {C}^{*}$-ALGEBRAS FROM
$\boldsymbol {C}^{*}$-ALGEBRAS FROM 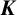 $\boldsymbol {K}$ GROUP REPRESENTATIONS
$\boldsymbol {K}$ GROUP REPRESENTATIONS