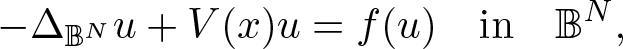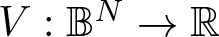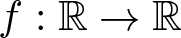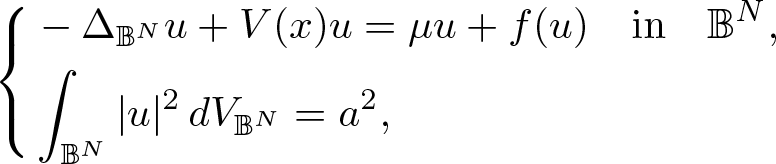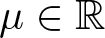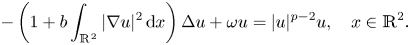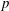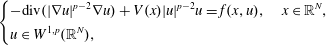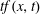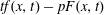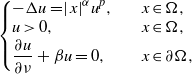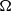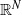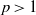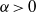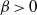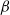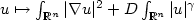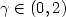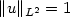Refine search
Actions for selected content:
5 results
On the existence of positive solutions to some classes of elliptic problems in Hyperbolic space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 July 2025, pp. 1-41
-
- Article
- Export citation
Necessary and sufficient conditions for ground state solutions to planar Kirchhoff-type equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 March 2024, pp. 1-22
-
- Article
- Export citation
GROUND STATE SOLUTIONS FOR
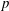 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-SUPERLINEAR
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-SUPERLINEAR 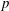 $p$-LAPLACIAN EQUATIONS
$p$-LAPLACIAN EQUATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 15 May 2014, pp. 48-62
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
THE ROBIN PROBLEM FOR THE HÉNON EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 27 June 2013, pp. 1-11
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
On a semilinear variational problem
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 09 October 2009, pp. 86-101
- Print publication:
- January 2011
-
- Article
- Export citation