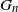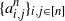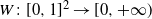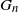Refine search
Actions for selected content:
3 results
Global stability for McKean–Vlasov equations on large networks
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 08 November 2024, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The k-core in percolated dense graph sequences
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 08 October 2024, pp. 298-318
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Breaking of ensemble equivalence for dense random graphs under a single constraint
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 1181-1200
- Print publication:
- December 2023
-
- Article
- Export citation