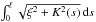Search

Skip to main content Accessibility help

Menu links

Browse

Subjects

Subjects (A-D)

Subjects (E-K)

Subjects (L-O)

Subjects (P-Z)

Open access

All open access publishing

Journals

Explore

Open access

Collections

Books

Explore

Collections

Collections (cont.)

Elements

Explore

Subjects (A-E)

Subjects (F-O)

Subjects (P-Z)

Textbooks

Explore

Collections

Book collections

Book collections (cont.)

Journal collections

Series

All series

Partners

Partners

Partners (cont.)

Services

About

About Cambridge Core

Environment and sustainability

Guides

Help

Agents

Services for agents

Authors

Journals

Journals (cont.)

Journals (cont.)

Books

Corporates

Corporates

Editors

Information

Resources

Librarians

Information

Products

Tools

Resources

Peer review

Peer review

Publishing ethics

Journals

Publishing ethics guidelines for journals
Core editorial policies for journals
Authorship and contributorship for journals
Affiliations for journals
Research ethics for journals
Competing interests and funding for journals

Journals (cont.)

Books

Books (cont.)

Publishing partners

Publishing partners

Publishing partners (cont.)

Open research

Open access policies

Open access policies

Journals

Books and Elements

Open access publishing

About open access

Open access resources

Open research initiatives

Research transparency

Journal flips

Flip it Open

Open access funding

Open access funding

Cambridge Open Engage

Cambridge Open Engage

Home
Search

Only show content I have access to (0)

Articles (1)

Over 3 years (1)

From year:

To year:

Apply

Mathematics (1)

generalized pontryagin maximum principle

ESAIM: Control, Optimisation and Calculus of Variations (1)

View selected items
Save to my bookmarks
Export citations
Download PDF (zip)
Save to Kindle
Save to Dropbox
Save to Google Drive
Save content to
To save content items to your account, please confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your account. Find out more about saving content to .

To save content items to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Please be advised that item(s) you selected are not available.
You are about to save
Your Kindle email address

Please provide your Kindle email.

@free.kindle.com @kindle.com (service fees apply)

By using this service, you agree that you will only keep content for personal use, and will not openly distribute them via Dropbox, Google Drive or other file sharing services

1 results

Curve cuspless reconstruction via sub-Riemannian geometry ∗∗∗
Ugo Boscain, Remco Duits, Francesco Rossi, Yuri Sachkov
Journal:

ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 3 / July 2014

Published online by Cambridge University Press:

27 May 2014, pp. 748-770

Print publication:

July 2014
- Article
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation
We consider the problem of minimizing \hbox{$\int_{0}^\ell \sqrt{\xi^2 +K^2(s)}\, {\rm d}s $}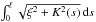 ${^{\int}}_{0}^{ℓ} \sqrt{ξ^{2} + K^{2} (s)} d s$ for a planar curve having fixedinitial and final positions and directions. The total length ℓ is free. Heres is thearclength parameter, K(s) is the curvature of the curveand ξ > 0 is a fixed constant. This problem comes from a model of geometry ofvision due to Petitot, Citti and Sarti. We study existence of local and global minimizersfor this problem. We prove that if for a certain choice of boundary conditions there is noglobal minimizer, then there is neither a local minimizer nor a geodesic. We finally giveproperties of the set of boundary conditions for which there exists a solution to theproblem.