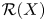We extend the notions of μ*-sequences and Tjurina numbers of functions to the framework of Bruce–Roberts numbers, that is, to pairs formed by the germ at 0 of a complex analytic variety X ⊆ ℂn and a finitely ${\mathcal R}(X)$-determined analytic function germ f : (ℂn, 0) → (ℂ, 0). We analyze some fundamental properties of these numbers.

It is proved that flatness of an analytic mapping germ from a complete intersection is determined by its sufficiently high jet. As a consequence, one obtains finite determinacy of complete intersections. It is also shown that flatness and openness are stable under deformations.

Let $f:({\mathbb R}^n,0)\rightarrow(\Bbb R^p,0)$ be a $C^\infty$ map-germ. We define $f$ to be finitely, or $\infty$-, $\mathcal A$-determined, if there exists an integer $m$ such that all germs $g$ with $j^mg(0)=j^mf(0)$, or if all germs $g$ with the same infinite Taylor series as $f$, respectively, are $\mathcal A$-equivalent to $f$. For any integer $k$, $0\le k<\infty$, we can consider $\mathcal A$\rq s $C^k$ counterpart (consisting of $C^k$ diffeomorphisms)$\mathcal A^{(k)}$, and we can define the notion of finite, or $\infty$-,$\mathcal A^{(k)}$-determinacy in a similar manner.Consider the following conditions for a $C^{\infty}$ germ $f$: (a$_k$) $f$ is $\infty$-$\mathcal A^{(k)}$-determined, (b$_k$)$f$ is finitely$\mathcal A^{(k)}$-determined, (t) $m_n^{\infty}\theta(f)\subset tf(m_n\theta(n))+\omega f(m_p\theta(p))$, (g)there exists a representative $ f:U\rightarrow\Bbb R^p$ defined on some neighbourhood $U$ of 0 in $\Bbb R^n$ such that the multigerm of $f$ is stable at every finite set $S\subset U-\lbrace0\rbrace$, and (g$^\prime$) every $f^\prime $ with $j^\infty f^\prime(0)=j^\infty f(0)$ satisfies condition (g). Wealso define a technical condition which will imply condition $(\mbox{g})$ above. This condition is a collection of $p+1$ \Lojasiewicz inequalities which express that the multigerm of $f$ is stable at any finite set of points outside 0and only becomes unstable at afinite rate when we approach 0. We will denote this condition by (e). With this notation we prove the following.For any $ C^\infty$ map germ $f:(\Bbb R^n,0)\rightarrow(\Bbb R^p,0)$ the conditions(e), (t), (g$'$) and ($\mbox{a}_{\infty}$) are equivalent conditions. Moreover, each of these conditions is equivalent to any of($\mbox{a}_k$) $(p+1\le k<\infty)$, ($\mbox{b}_k$) $(p+1\le k<\infty)$.

1991 Mathematics Subject Classification: 58C27.