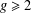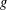Refine search
Actions for selected content:
1 results
SYSTOLIC FILLINGS OF SURFACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 28 August 2018, pp. 502-511
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
-
A filling of a closed hyperbolic surface is a set of simpleclosed geodesics whose complement is a disjoint union of hyperbolicpolygons. The systolic length is the length of a shortestessential closed geodesic on the surface. A geodesic is called systolic, ifthe systolic length is realised by its length. For every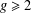
$g\geq 2$ , we construct closed hyperbolic surfaces of genus 
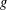$g$ whose systolic geodesics fill the surfaces withcomplements consisting of only two components. Finally, we remark that onecan deform the surfaces obtained to increase the systole.
