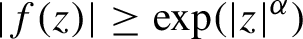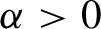Refine search
Actions for selected content:
1 results
Exponential polynomials with Fatou and non-escaping sets of finite Lebesgue measure
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 20 November 2020, pp. 3821-3840
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- Export citation
-
We give conditions ensuring that the Fatou set and the complement of the fast escaping set of an exponential polynomial f both have finite Lebesgue measure. Essentially, these conditions are designed such that
$|f(z)|\ge \exp (|z|^\alpha )$ for some 
$\alpha>0$ and all z outside a set of finite Lebesgue measure.
