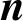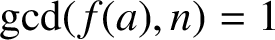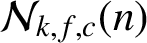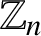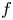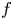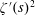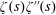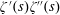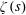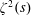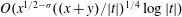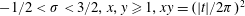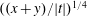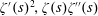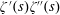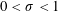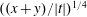Refine search
Actions for selected content:
9 results
11 - Geometric approach
-
- Book:
- Linear Cryptanalysis
- Published online:
- 17 December 2025
- Print publication:
- 20 November 2025, pp 150-167
-
- Chapter
- Export citation
Bilinear Kloosterman sums in function fields and the distribution of irreducible polynomials
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 20 December 2024, pp. 1-26
-
- Article
- Export citation
SUMS OF POLYNOMIAL-TYPE EXCEPTIONAL UNITS MODULO
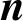 $\boldsymbol {n}$
$\boldsymbol {n}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 21 July 2021, pp. 202-211
- Print publication:
- April 2022
-
- Article
- Export citation
Dual exponential polynomials and a problem of Ozawa
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 16 June 2021, pp. 701-719
- Print publication:
- June 2022
-
- Article
- Export citation
EXPONENTIAL SUMS AND ADDITIVE COMBINATORICS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 09 November 2020, pp. 506-508
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
Titchmarsh’s Method for the Approximate Functional Equations for
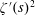 $\unicode[STIX]{x1D701}^{\prime }(s)^{2}$,
$\unicode[STIX]{x1D701}^{\prime }(s)^{2}$, 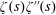 $\unicode[STIX]{x1D701}(s)\unicode[STIX]{x1D701}^{\prime \prime }(s)$, and
$\unicode[STIX]{x1D701}(s)\unicode[STIX]{x1D701}^{\prime \prime }(s)$, and 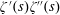 $\unicode[STIX]{x1D701}^{\prime }(s)\unicode[STIX]{x1D701}^{\prime \prime }(s)$
$\unicode[STIX]{x1D701}^{\prime }(s)\unicode[STIX]{x1D701}^{\prime \prime }(s)$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 1465-1493
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Multiplicative Energy of Shifted Subgroups and Bounds On Exponential Sums with Trinomials in Finite Fields
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 6 / 01 December 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1319-1338
- Print publication:
- 01 December 2018
-
- Article
-
- You have access
- Export citation
A NOTE ON SOME CHARACTER SUMS OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 30 April 2015, pp. 32-43
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
Notes on Erdös-Turán inequality
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 1 / August 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 51-57
- Print publication:
- August 1999
-
- Article
-
- You have access
- Export citation