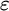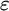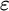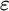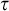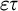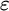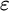Refine search
Actions for selected content:
2 results
A SIMPLIFIED PROOF OF THE EPSILON THEOREMS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 10 July 2023, pp. 1248-1263
- Print publication:
- December 2024
-
- Article
- Export citation
EPSILON THEOREMS IN INTERMEDIATE LOGICS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 682-720
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation