In this paper, we characterize Jordan $*$ -derivations of a 2-torsion free, finite-dimensional semiprime algebra $R$ with involution $*$ . To be precise, we prove the following. Let 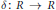$\delta :\,R\,\to \,R$ be a Jordan $*$ -derivation. Then there exists a $*$ -algebra decomposition 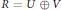$R\,=\,U\,\oplus \,V$ such that both 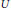$U$ and 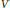$V$ are invariant under $\delta $ . Moreover, $*$ is the identity map of 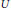$U$ and 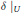$\delta {{|}_{U}}$ is a derivation, and the Jordan $*$ -derivation 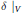$\delta {{|}_{V}}$ is inner. We also prove the following. Let $R$ be a noncommutative, centrally closed prime algebra with involution $*$ , char 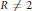$R\,\ne \,2$ , and let $\delta $ be a nonzero Jordan $*$ -derivation of $R$ . If $\delta $ is an elementary operator of $R$ , then 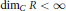${{\dim}_{C}}\,R\,<\,\infty $ and $\delta $ is inner.

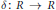
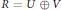
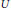
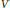
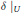
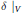
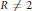
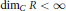
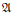Let A be a unital C*-algebra with the canonical (H) C*-bundle over the maximal ideal space of the centre of A, and let E(A) be the set of all elementary operators on A. We consider derivations on A which lie in the completely bounded norm closure of E(A), and show that such derivations are necessarily inner in the case when each fibre of is a prime C*-algebra. We also consider separable C*-algebras A for which is an (F) bundle. For these C*-algebras we show that the following conditions are equivalent: E(A) is closed in the operator norm; A as a Banach module over its centre is topologically finitely generated; fibres of have uniformly finite dimensions, and each restriction bundle of over a set where its fibres are of constant dimension is of finite type as a vector bundle.

We consider elementary operators on centrally closed prime algebras that are Lie (or Jordan) homomorphisms or commutativity preservers.

AMS 2000 Mathematics subject classification: Primary 16N60. Secondary 16R50; 47B47