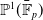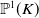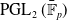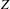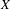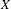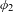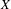Refine search
Actions for selected content:
30 results
1 - Introduction to Dynamical Systems for Biology
-
- Book:
- Theoretical Biology of the Cell
- Published online:
- 05 June 2025
- Print publication:
- 19 June 2025, pp 1-40
-
- Chapter
- Export citation

Theoretical Biology of the Cell
- A Dynamical-Systems Perspective
-
- Published online:
- 05 June 2025
- Print publication:
- 19 June 2025
Coupling results and Markovian structures for number representations of continuous random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 28 April 2025, pp. 1340-1359
- Print publication:
- December 2025
-
- Article
- Export citation
2 - Dynamical Systems
- from Part I - Lectures on Basics with Examples
-
- Book:
- Time-Variant and Quasi-separable Systems
- Published online:
- 24 October 2024
- Print publication:
- 31 October 2024, pp 21-40
-
- Chapter
- Export citation
6 - Atmospheric Predictability and Ensemble Forecasting
-
- Book:
- Earth System Modeling, Data Assimilation and Predictability
- Published online:
- 21 March 2025
- Print publication:
- 31 October 2024, pp 224-282
-
- Chapter
- Export citation

Time-Variant and Quasi-separable Systems
- Matrix Theory, Recursions and Computations
-
- Published online:
- 24 October 2024
- Print publication:
- 31 October 2024
1 - Introduction
-
- Book:
- Künneth Geometry
- Published online:
- 07 December 2023
- Print publication:
- 21 December 2023, pp 1-12
-
- Chapter
- Export citation
2 - Dynamical Systems and Markov Processes
- from Part I - Concepts from Modeling, Inference, and Computing
-
- Book:
- Data Modeling for the Sciences
- Published online:
- 17 August 2023
- Print publication:
- 31 August 2023, pp 40-107
-
- Chapter
- Export citation
16 - Miscellaneous Topics Related to Rectifiability
-
- Book:
- Rectifiability
- Published online:
- 19 December 2022
- Print publication:
- 12 January 2023, pp 143-148
-
- Chapter
-
- You have access
- Open access
- Export citation
Chapter 6 - Applying Dynamical Systems Theory to Model the Mind
- from Part II - Models and Tools
-
- Book:
- Cognitive Science
- Published online:
- 10 November 2022
- Print publication:
- 10 November 2022, pp 114-129
-
- Chapter
- Export citation
Automorphism groups of endomorphisms of
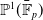 $\mathbb{P}^1 (\bar{\mathbb{F}}_p)$
$\mathbb{P}^1 (\bar{\mathbb{F}}_p)$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 13 July 2022, pp. 222-255
- Print publication:
- January 2023
-
- Article
- Export citation
8 - Further Applications
- from Part Three - Complementary Topics
-
- Book:
- The Christoffel–Darboux Kernel for Data Analysis
- Published online:
- 31 March 2022
- Print publication:
- 07 April 2022, pp 115-124
-
- Chapter
- Export citation
New approach to weighted topological entropy and pressure
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 28 January 2022, pp. 1004-1034
- Print publication:
- March 2023
-
- Article
- Export citation
BEYOND SLOW-FAST: RELAXATION OSCILLATIONS IN SINGULARLY PERTURBED NONSMOOTH SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 10 June 2021, pp. 342-343
- Print publication:
- October 2021
-
- Article
-
- You have access
- Export citation
LINEAR RESPONSE IN DYNAMICAL SYSTEMS: OPTIMISATION AND FINITE-TIME COHERENT SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 09 October 2020, pp. 515-516
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
INVARIANT HYPERSURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 17 August 2020, pp. 713-739
- Print publication:
- March 2022
-
- Article
- Export citation
2 - Algorithmic randomness in ergodic theory
-
-
- Book:
- Algorithmic Randomness
- Published online:
- 07 May 2020
- Print publication:
- 07 May 2020, pp 40-57
-
- Chapter
- Export citation
Positive contagion and the macrostructures of generalized balance
-
- Journal:
- Network Science / Volume 7 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 20 September 2019, pp. 445-458
-
- Article
-
- You have access
- Open access
- Export citation
8 - Semigroups and Dynamics
-
- Book:
- Semigroups of Linear Operators
- Published online:
- 27 July 2019
- Print publication:
- 15 August 2019, pp 149-165
-
- Chapter
- Export citation
New perspectives on the Erlang-A queue
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 22 July 2019, pp. 268-299
- Print publication:
- March 2019
-
- Article
- Export citation