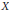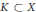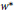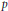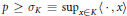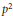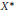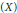Refine search
Actions for selected content:
1 results
On Super Weakly Compact Convex Sets and Representation of the Dual of the Normed Semigroup They Generate
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 2 / 01 June 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 272-282
- Print publication:
- 01 June 2013
-
- Article
-
- You have access
- Export citation
-
In this note, we first give a characterization of super weakly compact convex sets of a Banach space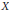
$X$ : a closed bounded convex set 
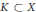$K\,\subset \,X$ is super weakly compact if and only if there exists a 
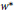${{w}^{*}}$ lower semicontinuous seminorm 
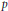$P$ with 
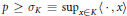$P\,\ge \,{{\sigma }_{K}}\,\equiv \,{{\sup }_{x\in K}}\left\langle \,\cdot \,,\,x \right\rangle $ such that 
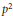${{P}^{2}}$ is uniformly Fréchet differentiable on each bounded set of 
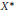${{X}^{*}}$ . Then we present a representation theoremfor the dual of the semigroup swcc 
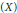$\left( X \right)$ consisting of all the nonempty super weakly compact convex sets of the space 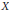$X$ .
