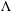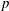Refine search
Actions for selected content:
6 results
Appendix E - Differential Forms on Infinite-Dimensional Manifolds
-
- Book:
- An Introduction to Infinite-Dimensional Differential Geometry
- Published online:
- 08 December 2022
- Print publication:
- 22 December 2022, pp 231-243
-
- Chapter
-
- You have access
- Open access
- Export citation
The Steklov Problem on Differential Forms
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 417-435
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
DIFFERENTIAL FORMS ON STRATIFIED SPACES II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 311-318
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Long Time Behaviour of Leafwise Heat Flow for Riemannian Foliations
-
- Journal:
- Compositio Mathematica / Volume 125 / Issue 2 / January 2001
- Published online by Cambridge University Press:
- 04 December 2007, pp. 129-153
- Print publication:
- January 2001
-
- Article
-
- You have access
- Export citation
DIFFERENTIAL FORMS ON FREE AND ALMOST FREE DIVISORS
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 81 / Issue 3 / November 2000
- Published online by Cambridge University Press:
- 03 November 2000, pp. 587-617
- Print publication:
- November 2000
-
- Article
- Export citation
Integrals on a moving manifold and geometrical probability
-
- Journal:
- Advances in Applied Probability / Volume 9 / Issue 3 / September 1977
- Published online by Cambridge University Press:
- 01 July 2016, pp. 588-603
- Print publication:
- September 1977
-
- Article
- Export citation